1D diagnostics

xgc.oneddiag.bp contains diagnostics of flux-surface averaged quantities.

Remarks

There are two radial discretizations in the 1D diagnostics: one set by the input parameter sml_00_npsi and one set by the number of closed flux surfaces crossing the lower-field-side midplane (# flux surfaces). There can be narrow flux surfaces that do not cross the lower-field-side midplane and these are not included in the default 1D diagnostics.

For neoclassical simulations (XGCa) it is advisable to calculate the proper flux-surface averaged fluxes by using the 2D diagnostics, and either the node volumes in Mesh or the flux-surface averaging matrix in Matrix operations. The reason is that the neoclassical fluxes are so small that it is important to accurately split the adiabatic and non-adiabatic parts of the distribution function.

‘# outputs’ below is ‘# of time steps.’ The time steps are usually incremental, but a restart of simulations from checkpoint files will break this. ‘step’ will indicate the time steps of the simulation and ‘time’ will tell the physical time of the time step.

In the variable names, the prefix e_, i_, i2_, tells the plasma species. The suffixes of the plasma quantities are _1d or _df_1d. _1d if for full-f quantities and _df_1d is for total-f quantities. Full-f (_1d) quantities are usually noisy and do not include collision/source physics. These quantities are directly linked to marker particles. Total-f (_df_1d) quantities are actual plasma quantities for total-f simulations. For reduced delta-f simulations, _df_1d will give perturbed quantities, but not always - some of the variables are not adequate for reduced delta-f simulation.

xgc.oneddiag.bp
Printed when: diag_1d_on=.true..   Output frequency: diag_1d_period.

Output	Dimension	Units	Description
cden00_1d	# outputs \(\times\) sml_00_npsi	\({\mathrm{m}}^{-3}\)	charge density in psi00 (iden00_1d - eden00_1d)
e_gc_density_1d i_gc_density_1d e_gc_density_df_1d i_gc_density_df_1d	# outputs \(\times\) # flux surfaces	\({\mathrm{m}}^{-3}\)	Electron/Ion density of gyro-center. Note that the gyro-center density is close to the actual plasma density for electrons, but polarization density could be significantly large for ions and the gyro-center density plus the polarization density is the actual ion density.
e_gc_poloidal_flow_1d i_gc_poloidal_flow_1d e_gc_poloidal_flow_df_1d i_gc_poloidal_flow_df_1d	# outputs \(\times\) # flux surfaces	\({\mathrm{m/s}}\)	Flux averaged poloidal flow of gyro-center. This differs from the poloidal flow by the diamagnetic flow.
e_gc_toroidal_flow_1d i_gc_toroidal_flow_1d e_gc_toroidal_flow_df_1d i_gc_toroidal_flow_df_1d	# outputs \(\times\) # flux surfaces	\({\mathrm{m/s}}\)	Flux averaged toroidal flow of gyro-center. This differs from the toroidal flow by the diamagnetic flow.
e_grad_psi_sqr_1d i_grad_psi_sqr_1d	# outputs \(\times\) # flux surfaces	\({\mathrm{(Tm)^2}}\)	Particle average of \({\mathrm{|\nabla \psi|^2}}\) for each flux surfaces. Roughly flux average of \({\mathrm{|\nabla \psi|^2}}\) This is usually used for converting \({\mathrm{{\partial \psi}}\) to \({\mathrm{\partial r}}\)
e_grad_psi_sqr_df_1d i_grad_psi_sqr_df_1d	# outputs \(\times\) # flux surfaces	Units	Do not use these variables. Use ‘_1d’ to get Flux average of \({\mathrm{|\nabla \psi|^2}}\)
e_parallel_flow_1d i_parallel_flow_1d e_parallel_flow_df_1d i_parallel_flow_df_1d	# outputs \(\times\) # flux surfaces	\({\mathrm{m/s}}\)	Parallel flow velocities
e_parallel_mean_en_1d i_parallel_mean_en_1d e_parallel_mean_en_df_1d i_parallel_mean_en_df_1d	# outputs \(\times\) # flux surfaces	\({\mathrm{eV}}\)	Parallel kinetic energy in eV. \(<0.5 m v^2>\) For parallel temperature, mean flow energy should be subtracted.
e_perp_temperature_1d i_perp_temperature_1d e_perp_temperature_df_1d i_perp_temperature_df_1d	# outputs \(\times\) # flux surfaces	\(\mathrm{eV}\)	Perpendicular temperature \(<\mu B>\)
e_poloidal_ExB_flow_1d i_poloidal_ExB_flow_1d e_poloidal_ExB_flow_df_1d i_poloidal_ExB_flow_df_1d	# outputs \(\times\) # flux surfaces	\({\mathrm{m/s}}\)	Particle average of poloidal flow by \(E \times B\) drift.
e_radial_en_flux_1d i_radial_en_flux_1d e_radial_en_flux_df_1d i_radial_en_flux_df_1d	# outputs \(\times\) # flux surfaces	\({\mathrm{JTm^2s^{-1}}}\)	Particle averaged radial energy flux in \(\psi\) space. \(<E V \cdot \nabla \psi>\) Averaged \(\nabla \psi\) is required to get radial flux in real space (J m/s)’
e_radial_en_flux_3db_1d i_radial_en_flux_3db_1d e_radial_en_flux_3db_df_1d i_radial_en_flux_3db_df_1d	# outputs \(\times\) # flux surfaces	\({\mathrm{JTm^2s^{-1}}}\)	Particle averaged radial energy flux by \(\delta B\) in \(\psi\) space. \(<E V_{\delta B} \cdot \nabla \psi>\) Averaged \(\nabla \psi\) is required to get radial flux in real space (J m/s)’
e_radial_en_flux_ExB_1d i_radial_en_flux_ExB_1d e_radial_en_flux_ExB_df_1d i_radial_en_flux_ExB_df_1d	# outputs \(\times\) # flux surfaces	\({\mathrm{JTm^2s^{-1}}}\)	Particle averaged radial energy flux by \(E \times B\) in \(\psi\) space. \(<E V_{E \times B} \cdot \nabla \psi>\) Averaged \(\nabla \psi\) is required to get radial flux in real space (J m/s)’
e_radial_flux_1d i_radial_flux_1d e_radial_flux_df_1d i_radial_flux_df_1d	# outputs \(\times\) # flux surfaces	\({\mathrm{Tm^2 s^{-1}}}\)	Particle averaged radial drift in \(\psi\) space. \(<V \cdot \nabla \psi>\) Averaged \(\nabla \psi\) is required to get radial flux in real space (m/s)’
e_radial_flux_3db_1d i_radial_flux_3db_1d e_radial_flux_3db_df_1d i_radial_flux_3db_df_1d	# outputs \(\times\) # flux surfaces	\({\mathrm{Tm^2 s^{-1}}}\)	Particle averaged radial drift by \(\delta B\) in \(\psi\) space. \(<V_{\delta B} \cdot \nabla \psi>\) Averaged \(\nabla \psi\) is required to get radial flux in real space (m/s)’
e_radial_flux_ExB_1d i_radial_flux_ExB_1d e_radial_flux_ExB_df_1d i_radial_flux_ExB_df_1d	# outputs \(\times\) # flux surfaces	\({\mathrm{Tm^2 s^{-1}}}\)	Particle averaged radial drift by \(E \times B\) in \(\psi\) space. \(<V_{E \times B} \cdot \nabla \psi>\) Averaged \(\nabla \psi\) is required to get radial flux in real space (m/s)’
e_radial_mom_flux_1d i_radial_mom_flux_1d e_radial_mom_flux_df_1d i_radial_mom_flux_df_1d	# outputs \(\times\) # flux surfaces	\({\mathrm{T m^3 s^{-2}}}\)	Particle averaged toroidal momentum flux in \(\psi\) space. \(<V_{tor} V \cdot \nabla \psi>\) Averaged \(\nabla \psi\) is required to get radial flux in real space (m/s)’
e_radial_mom_flux_ExB_1d i_radial_mom_flux_ExB_1d e_radial_mom_flux_ExB_df_1d i_radial_mom_flux_ExB_df_1d	# outputs \(\times\) # flux surfaces	\({\mathrm{T m^3 s^{-2}}}\)	Particle averaged toroidal momentum flux by \(E \times B\) in \(\psi\) space. \(<V_{tor} V_{E \times B} \cdot \nabla \psi>\) Averaged \(\nabla \psi\) is required to get radial flux in real space (m/s)’
e_tor_angular_momentum_1d i_tor_angular_momentum_1d e_tor_angular_momentum_df_1d i_tor_angular_momentum_df_1d	# outputs \(\times\) # flux surfaces	\(\mathrm{m^2 s^{-1}}\)	Toroidal angular momentum (without mass) < V_{tor} R >
e_vpar_x_B_1d i_vpar_x_B_1d e_vpar_x_B_df_1d i_vpar_x_B_df_1d	# outputs \(\times\) # flux surfaces	\({\mathrm{T m s^{-1}}}\)	For bootstrap current \(<V_{||} B>\)
eden00_1d iden00_1d	# outputs \(\times\) sml_00_npsi	\({\mathrm{m}}^{-3}\)	perturbed density of electron/ion. Even though the suffixes are ‘_1d’, these are total-f quantities for total-f simulations.
gsamples	# outputs	N.A.	Radial array size of ‘00’ variables
pot00_1d	# outputs \(\times\) sml_00_npsi	V	Flux averaged electrostatic potential
psi	# outputs \(\times\) # flux surfaces	Normalized	Normalized poloidal magnetic flux at each output on each flux surface.
psi00	# outputs \(\times\) sml_00_npsi	\(\mathrm{T m^2}\)	Unnormalized poloidal magnetic flux at each output on each flux surface.
psi_mks	# outputs \(\times\) # flux surfaces	\(\mathrm{T m^2}\)	Unnormalized poloidal magnetic flux at each output on each flux surface.
samples	# outputs	N.A.	# flux surfaces
step	# outputs	Positive integer	(1, 2, …, # outputs) \(\times\) diag_1d_period, i.e. the simulation time steps when the diagnostics are printed.
time	# outputs	\(\mathrm{s}\)	Simulation time at each output in seconds.
tindex	# outputs	Positive integer	1, 2, …, # outputs

Usage example

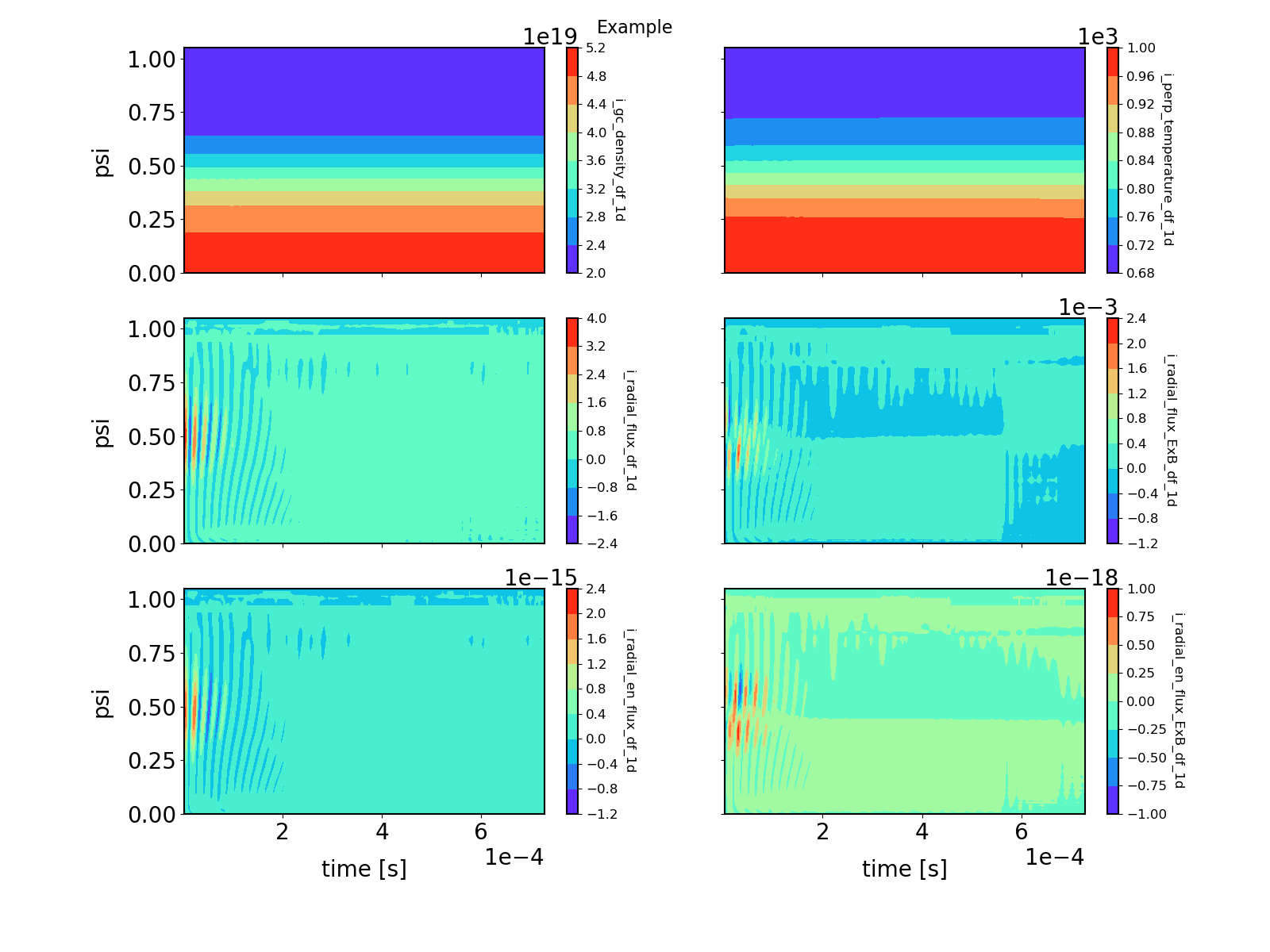
Time evolution of the radial profiles of flux-surface averaged density, temperature, and radial particle and energy fluxes.