current_drive.cpp File Reference

#include "push_physics.hpp"
#include "current_drive.hpp"

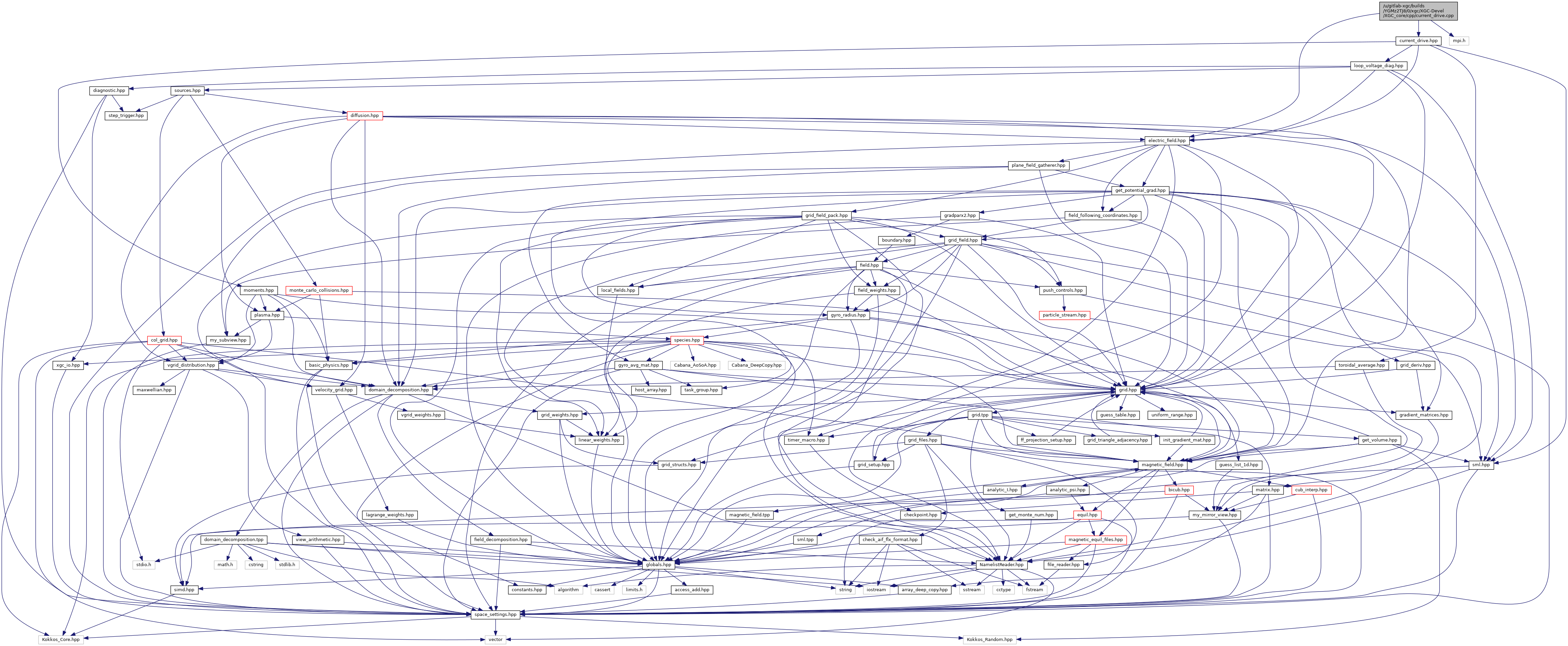
Include dependency graph for current_drive.cpp:

Functions
View< double *, CLayout, DeviceType >	calc_jpar0 (const Grid< DeviceType > &grid, const MagneticField< DeviceType > &magnetic_field)
KOKKOS_INLINE_FUNCTION double	parallel_spitzer_resistivity (double den, double te)

Function Documentation

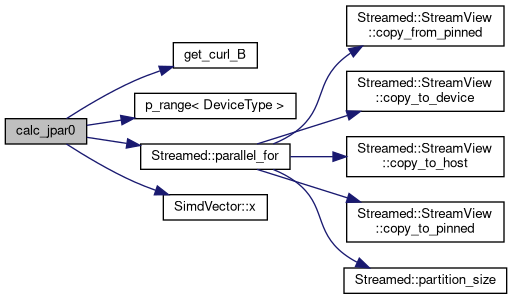
calc_jpar0()

View<double*,CLayout,DeviceType> calc_jpar0	(	const Grid< DeviceType > &	grid,
		const MagneticField< DeviceType > &	magnetic_field
	)

Here is the call graph for this function:

Here is the caller graph for this function:

parallel_spitzer_resistivity()

KOKKOS_INLINE_FUNCTION double parallel_spitzer_resistivity	(	double	den,
		double	te
	)

Evaluates the parallel Spitzer resistivity in \(\Omega m\) for given density and temperatures. Uses a simplified formula (NRL Formulary 2019, assuming \(T_e>10\) eV) because the logic to adjust V_loop is heuristic anyway.

Parameters

[in]	den	Plasma (electron) density in \(m^{-3}\), double
[in]	te	Electron temperature in eV, double

Here is the caller graph for this function: