This module contains functions to construct finite element matrices for Helmholtz type equations div(alpha grad(X)) + beta X = gamma, and evaluate div(grad_RZ(X)) and v.grad_RZ(X) operations. More...

Public Member Functions
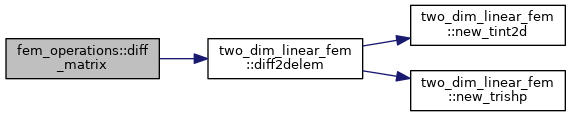
subroutine	eval_helm_matrix (fu, uu, grid, bc, op_mode)
	Evaluates \(-\nabla\cdot\nabla f(R,Z)\) (op_mode==1), or the FEM mass-matrix projection of a function in a linear finite element discretization. More...

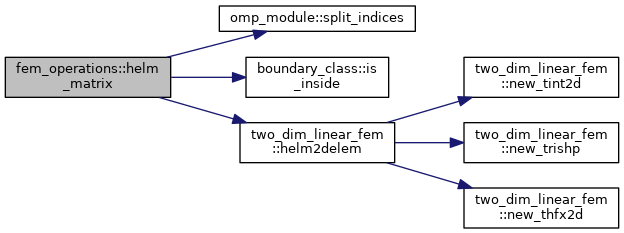
subroutine	b_dot_grad_u (bdotgradu, b1, b2, uu, grid)

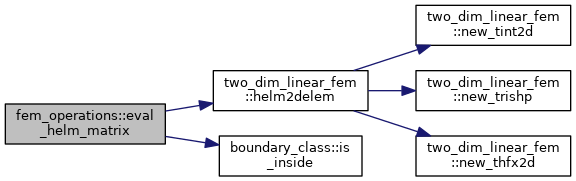
subroutine	helm_matrix (grid, Amat, solver_data, alpha, beta, ntor, set_bmat, bd, bcflag, xgc_petsc, xgc_petsc_bd, bs, idx, jdx, scale_vec, mat_assemble, ierr)
	This routine sets up the matrix for the LHS of a Helmholtz equation of the form \(\nabla\cdot\left( \alpha\nabla_\perp\phi\right) + \beta \phi\). The routine loops over triangles, evaluates the stiffness matrix of the problem for the element and then proceeds to populate the RHS matrix of the Helmholtz equation with the proper entries of the stiffness matrix. In order to limit the computing time spent on this, triangles that are completely outside of the mesh area assigned to an MPI rank are skipped. More...

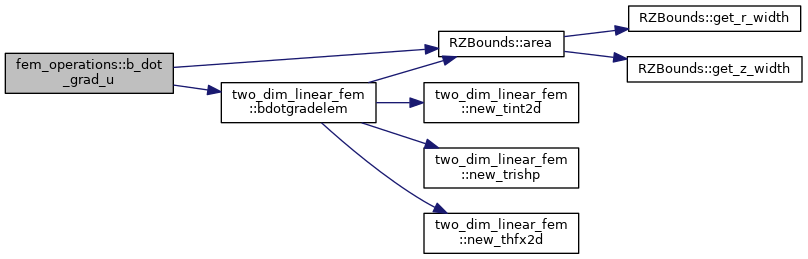
subroutine	diff_matrix (grid, Amat, D, pinch_v, pinch_factor, geo_factors, bd, bcflag, mass_flag, pinch_flag, indirect_pinch_flag, xgc_petsc, bs, idx, jdx, scale_vec, mat_assemble, ierr)
	Sets up the matrix elements of the RHS of Fick's law for diffusive transport with a pinch velocity: \( \frac{\partial F}{\partial t} = \nabla \cdot \left[ \boldsymbol{D}.\nabla F - F \boldsymbol{v}_p \right] \) with the diffusion tensor \( D_{ij} = D(\psi,\theta) (\hat{\boldsymbol{\psi}} \otimes \hat{\boldsymbol{\psi}}) \), where \( D(\psi,\theta) \) is a scalar function of the radial and poloidal coordinate, and \( \hat{\boldsymbol{\psi}}=\nabla\psi/\|\nabla \psi\|. @param[in] grid XGC grid data structure, type(grid_type) @param[out] Amat PETSc matrix to store the diffusion operator, (PETSc Mat) @param[in] D Diffusion coefficient, real(8) @param[in] pinch_v Particle pinch velocity, real(8) @param[in] pinch_factor Prefactor of the pinch term (1 in density and momentum, 5/3 in temp. eq.), real(8) @param[in] geo_factors Geometrical factors needed for diffusivity and pinch velocity @param[in] bd Solver boundary @param[in] bcflag Whether inhomogeneous boundary conditions are used, logical @param[in] mass_flag Whether the mass matrix or diffusion matrix is computed, logical @param[in] pinch_flag Whether a pinch term is included (\)({v}_p X) \(), logical @param[in] indirect_pinch_flag Whether an indirect pinch term (i.e., conservation term from pinch of lower moment) is included (\){v}_p X. More...

subroutine	fsa_21_t_matrix (grid, Amat, bcflag, xgc_petsc, petsc_xgc_bd, mat_assemble, ierr)
	This routine sets up the matrices for computing the flux surface average of a 2d scalar field: \( \langle \phi \rangle \). Contributions from the interior vertices and boundary vertices are handled by separate matrices. The matrices are constructed as the transpose of what is to be applied to vectors representing the interior vertices and boundary vertices. More...

subroutine	fsa_12_matrix (grid, Amat, bcflag, xgc_petsc, petsc_xgc_bd, mat_assemble, ierr)
	This routine sets up the matrices for placing 1d surface data onto a 2d scalar field. Placement onto interior vertices and boundary vertices are handled by separate matrices. More...

Detailed Description

This module contains functions to construct finite element matrices for Helmholtz type equations div(alpha grad(X)) + beta X = gamma, and evaluate div(grad_RZ(X)) and v.grad_RZ(X) operations.

Member Function/Subroutine Documentation

subroutine fem_operations::b_dot_grad_u	(	real (kind=8), dimension(grid%nnode), intent(out)	bdotgradu,
		real (kind=8), dimension(grid%nnode), intent(in)	b1,
		real (kind=8), dimension(grid%nnode), intent(in)	b2,
		real (kind=8), dimension(grid%nnode), intent(in)	uu,
		type(grid_type), intent(in)	grid
	)

Parameters

[out]	bdotgradu	Output function \(\boldsymbol{B}\cdot\nabla f(R,Z)\) (w/o toroidal component): \(B_R \partial f/\partial R + B_Z \partial f/\partial Z\), real(8)
[in]	b1	Major radial component of B ( \(B_R\)), real(8)
[in]	b2	Vertical component of B ( \(B_Z\)), real(8)
[in]	uu	Input function \(f(R,Z)\), real(8)
[in]	grid	XGC grid data structure, type(grid_type)

Here is the call graph for this function:

subroutine fem_operations::diff_matrix	(	type(grid_type), intent(in)	grid,
		intent(inout)	Amat,
		real (kind=8), dimension(grid%ntriangle), intent(in)	D,
		real (kind=8), dimension(grid%ntriangle), intent(in)	pinch_v,
		real (kind=8), intent(in)	pinch_factor,
		real (kind=8), dimension(3,grid%ntriangle), intent(in)	geo_factors,
		integer, dimension(grid%nnode), intent(in)	bd,
		logical, intent(in)	bcflag,
		logical, intent(in)	mass_flag,
		logical, intent(in)	pinch_flag,
		logical, intent(in)	indirect_pinch_flag,
		dimension(grid%nnode), intent(in)	xgc_petsc,
		intent(in)	bs,
		intent(in)	idx,
		intent(in)	jdx,
			scale_vec,
		logical, intent(in)	mat_assemble,
		intent(out)	ierr
	)

Sets up the matrix elements of the RHS of Fick's law for diffusive transport with a pinch velocity: \( \frac{\partial F}{\partial t} = \nabla \cdot \left[ \boldsymbol{D}.\nabla F - F \boldsymbol{v}_p \right] \) with the diffusion tensor \( D_{ij} = D(\psi,\theta) (\hat{\boldsymbol{\psi}} \otimes \hat{\boldsymbol{\psi}}) \), where \( D(\psi,\theta) \) is a scalar function of the radial and poloidal coordinate, and \( \hat{\boldsymbol{\psi}}=\nabla\psi/|\nabla \psi|. @param[in] grid XGC grid data structure, type(grid_type) @param[out] Amat PETSc matrix to store the diffusion operator, (PETSc Mat) @param[in] D Diffusion coefficient, real(8) @param[in] pinch_v Particle pinch velocity, real(8) @param[in] pinch_factor Prefactor of the pinch term (1 in density and momentum, 5/3 in temp. eq.), real(8) @param[in] geo_factors Geometrical factors needed for diffusivity and pinch velocity @param[in] bd Solver boundary @param[in] bcflag Whether inhomogeneous boundary conditions are used, logical @param[in] mass_flag Whether the mass matrix or diffusion matrix is computed, logical @param[in] pinch_flag Whether a pinch term is included (\)({v}_p X) \(), logical @param[in] indirect_pinch_flag Whether an indirect pinch term (i.e., conservation term from pinch of lower moment) is included (\){v}_p X.

Here is the call graph for this function:

Here is the caller graph for this function:

subroutine fem_operations::eval_helm_matrix	(	real (kind=8), dimension(grid%nnode), intent(out)	fu,
		real (kind=8), dimension(grid%nnode), intent(in)	uu,
		type(grid_type), intent(in)	grid,
		integer, dimension(grid%nnode), intent(in)	bc,
		integer, intent(in)	op_mode
	)

Evaluates \(-\nabla\cdot\nabla f(R,Z)\) (op_mode==1), or the FEM mass-matrix projection of a function in a linear finite element discretization.

Parameters

[out]	fu	Neg. Divergence of the gradient of the input function \(-\nabla\cdot\nabla f(R,Z)\), or \(\boldsymbol{M}\cdot f(R,Z)\), real(8)
[in]	uu	Input function \(f(R,Z)\), real(8)
[in]	grid	XGC grid data structure, type(grid_type)
[in]	bc	Boundary location
[in]	op_mode	Whether to calculate the Div(grad) (1), or mass matrix M.f (2)

Here is the call graph for this function:

Here is the caller graph for this function:

subroutine fem_operations::fsa_12_matrix	(	type(grid_type)	grid,
			Amat,
		logical, intent(in)	bcflag,
		dimension(grid%nnode), intent(in)	xgc_petsc,
		dimension(grid%nnode), intent(in)	petsc_xgc_bd,
		logical, intent(in)	mat_assemble,
		intent(out)	ierr
	)

This routine sets up the matrices for placing 1d surface data onto a 2d scalar field. Placement onto interior vertices and boundary vertices are handled by separate matrices.

Parameters

[in]	grid	XGC grid data structure, type(grid_type)
[out]	Amat	matrix for placing surface data onto interior vertices when bcflag=.false. or for placing surface data onto boundary vertices when bcflag = .true., PETSc Mat
[in]	bcflag	Flag to set either boundary matrix (true) or interior matrix (false), logical
[in]	xgc_petsc	Mapping from XGC vertex index to PETSc equation number, integer
[in]	petsc_xgc_bd	Mapping from PETSc equation number to vertex index on solver boundary, integer
[in]	mat_assemble	Whether to run the final matrix assembly, logical
[in]	ierr	Exit status, PETSc error type

Here is the call graph for this function:

Here is the caller graph for this function:

subroutine fem_operations::fsa_21_t_matrix	(	type(grid_type)	grid,
			Amat,
		logical, intent(in)	bcflag,
		dimension(grid%nnode), intent(in)	xgc_petsc,
		dimension(grid%nnode), intent(in)	petsc_xgc_bd,
		logical, intent(in)	mat_assemble,
		intent(out)	ierr
	)

This routine sets up the matrices for computing the flux surface average of a 2d scalar field: \( \langle \phi \rangle \). Contributions from the interior vertices and boundary vertices are handled by separate matrices. The matrices are constructed as the transpose of what is to be applied to vectors representing the interior vertices and boundary vertices.

Parameters

[in]	grid	XGC grid data structure, type(grid_type)
[out]	Amat	matrix for computing the contribution to the surface from interior vertices when bcflag=.false. and for computing the contribution to the surface from boundary vertices when bcflag=.true., PETSc Mat
[in]	bcflag	Flag to set either boundary matrix (true) or interior matrix (false), logical
[in]	xgc_petsc	Mapping from XGC vertex index to PETSc equation number, integer
[in]	petsc_xgc_bd	Mapping from PETSc equation number to vertex index on solver boundary, integer
[in]	mat_assemble	Whether to run the final matrix assembly, logical
[in]	ierr	Exit status, PETSc error type

Here is the call graph for this function:

Here is the caller graph for this function:

subroutine fem_operations::helm_matrix	(	type (grid_type), intent(in)	grid,
		intent(inout)	Amat,
		type (solver_init_data), intent(in)	solver_data,
		real (kind=8), dimension(grid%ntriangle), intent(in)	alpha,
		real (kind=8), dimension(grid%ntriangle), intent(in)	beta,
		integer, intent(in)	ntor,
		logical, intent(in)	set_bmat,
		integer, dimension(grid%nnode), intent(in)	bd,
		logical, intent(in)	bcflag,
		dimension(grid%nnode), intent(in)	xgc_petsc,
		dimension(grid%nnode), intent(in)	xgc_petsc_bd,
		intent(in)	bs,
		intent(in)	idx,
		intent(in)	jdx,
			scale_vec,
		logical, intent(in)	mat_assemble,
		intent(out)	ierr
	)

This routine sets up the matrix for the LHS of a Helmholtz equation of the form \(\nabla\cdot\left( \alpha\nabla_\perp\phi\right) + \beta \phi\). The routine loops over triangles, evaluates the stiffness matrix of the problem for the element and then proceeds to populate the RHS matrix of the Helmholtz equation with the proper entries of the stiffness matrix. In order to limit the computing time spent on this, triangles that are completely outside of the mesh area assigned to an MPI rank are skipped.

Parameters

[out]	Amat	Helmholtz matrix, PETSc Mat
[in]	solver_data	Data required for LHS setup (mag. field, etc.), type(solver_init_data)
[in]	alpha	Factor \(\alpha\) in Helmholtz operator at triangle center, real(8)
[in]	beta	Factor \(\beta\) in Helmholtz operator at triangle center, real(8)
[in]	ntor	Toroidal mode number or the Fourier mode to be solve (spectral solver only)
[in]	set_bmat	If true, the off-diagonal block of the 2x2 spectral solver matrix is constructed
[in]	grid	XGC grid data structure, type(grid_type)
[in]	bd	Solver boundary
[in]	bcflag	Flag indicating the type of boundary condition used, integer
[in]	xgc_petsc	Mapping from XGC vertex index to PETSc equation number, integer
[in]	xgc_petsc_bd	Mapping from XGC vertex index on the solver boundary to PETSc equation number
[in]	bs	Block size of the matrix in which to add the Helmholtz operator, PETSc int
[in]	idx	Block row index at which to add the Helmholtz operator, PETSc int
[in]	jdx	Block column index at which to add the Helmholtz operator, PETSc int
[in]	scale_vec	Scaling vector for scaling the rows of Amat, PETSc Vec
[in]	mat_assemble	Whether to run the final matrix assembly, logical
[in]	ierr	Exit status, PETSc error type

Here is the call graph for this function:

Here is the caller graph for this function:

The documentation for this module was generated from the following file:

/u/gitlab-xgc/builds/YGMz2TJ8/0/xgc/XGC-Devel/XGC_core/fem_ops.F90

Public Member Functions

Detailed Description

Member Function/Subroutine Documentation