#include "adios_macro.h"#include "t_coeff_mod_macro.h"#include "fftw3.f"
Data Types | |
| type | grid_class::grid_type |
Modules | |
| module | grid_class |
Functions/Subroutines | |
| subroutine | grid_class::set_fortran_flx_aif_format (old_flx_aif_format_int) |
| subroutine | grid_class::init_fortran_grid (grid_nnode_in, grid_ntriangle_in, grid_x_in, grid_rgn_in, grid_nd_in, grid_mapping_in, basis_in) |
| subroutine | grid_class::init_fortran_grid_surf (n_xpt, i_x1, i_x2, nsurf1, nsurf2, nsurf3a, nsurf3b, isurf_sep1, isurf_sep2, npsi_surf, surf_maxlen, num_non_aligned, surf_len, surf_idx, non_aligned_vert, non_aligned_nsurf, non_aligned_surf_idx) |
| subroutine | grid_class::init_secondary_grid_arrays (grid_psi_in, grid_grad_psi_in, grid_bfield_in) |
| subroutine | grid_class::init_guess_table_from_cpp (guess_n1, guess_list_len, guess_n_in, guess_min_in, guess_max_in, inv_guess_d_in, guess_list_in, guess_xtable_in, guess_count_in) |
| subroutine | grid_class::init_fortran_vols_and_areas (tr_area_h, tr_vol_h, node_vol_ff_h, node_vol_nearest_h, node_vol_h, node_area_h) |
| subroutine | grid_class::init_fortran_psi_grid_props (npsi_surf, psi_surf, npsi_surf2, psi_surf2, psi_surf_map) |
| subroutine | grid_class::alloc_fortran_gradient_mat_unit_vec (m, n, width) |
| subroutine | grid_class::set_fort_fsamat_ptr (m, n, width, value, eindex, nelement, m2, n2, width2, value2, eindex2, nelement2) |
| subroutine | grid_class::init_grid (grid) |
| Initializes the grid data structure from input files containing i) The (R,Z) coordinates of all vertices including whether they are wall vertices (.node file), ii) the connectivity of the vertices defining the triangles of the unstructured mesh (.ele file), iii) the flux-surface connectivity, i.e. which vertices are on the same flux-surface, and for vertices not aligned on flux-surfaces between which flux-surfaces those vertices lie. More... | |
| subroutine | grid_class::init_triangle (grid) |
| subroutine | grid_class::t_coeff (grid, itr, x, p) |
| subroutine | grid_class::t_coeff_mod (grid, xy, psiin, itr, p) |
| subroutine | grid_class::calc_gen_theta_psi (grid) |
| Calculates the average psi on the complete flux-surfaces and the generalized poloidal angle (=normalized poloidal arc length) More... | |
| subroutine | order_nodes (grid, isurf, isize, idx_start, theta, idx) |
| Sorts input SOL flux-surface according to the poloidal arclength l_theta where l_theta=0 at the outer midplane. More... | |
| subroutine | gen_pol_angle_single (i) |
| integer function | grid_class::get_nsurfs_for_avg () |
| subroutine | get_b_and_derivs_cyl (r, z, B_mag, br, bphi, bz, dbrdr, dbpdr, dbzdr, dbrdp, dbpdp, dbzdp, dbrdz, dbpdz, dbzdz) |
| subroutine | get_pe_info (mype, totalpe) |
| subroutine | search_tr2 (grid, xy, itr, p) |
| subroutine | search_tr_check_guess (grid, x, init, itr, p) |
| subroutine | write_gradient_mat (grid) |
| subroutine | fft_parallel_init (grid) |
| Initializes the parallelization of the field-aligned FFT filter. Since each flux-surface is filtered separately, the flux-surfaces are distributed among the MPI ranks in the inter-plane communicator (sml_intpl_comm). To achieve approximately even workload, the distribution of flux-surfaces, tries to assign equal numbers of vertices to each rank. More... | |
| subroutine | fourier_filter_n_m_range_parallel (nphi, ntor_min, ntor_max, ntor_min_real, ntor_max_real, bands_on_int, mpol_min, mpol_max, x, op_mode, num_mres_q, inpsi, outpsi, bd_width, div_mix_int) |
| Toroidal-poloidal Fourier filter for the regions 1 and 2 This version of the filter is parallelized to a high degree for optimal performance, and allows for multiple toroidal mode numbers. Removes high poloidal mode numbers from flux-surfaces while retaining small scale poloidal variations close to the divertor plates. This is achieved by applying a window function that removes the near-divertor part from the data. The windowed data is then low-pass filtered and the high-m variations are removed by calculating x_filtered = (1-win)*x - win*x_filtered. More... | |
| subroutine | fourier_filter_set_nonaligned (grid, x) |
| real(kind=8) function | fourier_filter_damp_fac (psi, inpsi, outpsi, bd_width) |
| Evaluate a damping factor for the boundary condition of the Fourier filter functions. More... | |
Variables | |
| integer, parameter | grid_class::grid_rgn_wall = 100 |
| real(8), parameter | grid_class::grid_search_tr2_psi_null = -1D10 |
| integer, parameter | grid_class::grid_min_surf_size = 5 |
| type(grid_type), target | grid_class::grid_global |
Function/Subroutine Documentation
◆ fft_parallel_init()
| subroutine fft_parallel_init | ( | type(grid_type), intent(inout) | grid | ) |
Initializes the parallelization of the field-aligned FFT filter. Since each flux-surface is filtered separately, the flux-surfaces are distributed among the MPI ranks in the inter-plane communicator (sml_intpl_comm). To achieve approximately even workload, the distribution of flux-surfaces, tries to assign equal numbers of vertices to each rank.
- Parameters
-
[in,out] grid grid data structure, type(grid_type)

◆ fourier_filter_damp_fac()
| real (kind=8) function fourier_filter_damp_fac | ( | real (kind=8), intent(in) | psi, |
| real (kind=8), intent(in) | inpsi, | ||
| real (kind=8), intent(in) | outpsi, | ||
| real (kind=8), intent(in) | bd_width | ||
| ) |
Evaluate a damping factor for the boundary condition of the Fourier filter functions.
- Parameters
-
[in] psi Input poloidal flux, real(8) [in] inpsi Inner filter boundary, real(8) [in] outpsi Outer filter boundary, real(8) [in] bd_width Boundary width, real(8)
◆ fourier_filter_n_m_range_parallel()
| subroutine fourier_filter_n_m_range_parallel | ( | integer, intent(in), value | nphi, |
| integer, intent(in), value | ntor_min, | ||
| integer, intent(in), value | ntor_max, | ||
| integer, intent(in), value | ntor_min_real, | ||
| integer, intent(in), value | ntor_max_real, | ||
| integer, intent(in), value | bands_on_int, | ||
| integer, intent(in), value | mpol_min, | ||
| integer, intent(in), value | mpol_max, | ||
| real (kind=8), dimension(grid%nnode), intent(inout) | x, | ||
| integer, intent(in), value | op_mode, | ||
| integer, intent(in), value | num_mres_q, | ||
| real (kind=8), intent(in), value | inpsi, | ||
| real (kind=8), intent(in), value | outpsi, | ||
| real (kind=8), intent(in), value | bd_width, | ||
| integer, intent(in), value | div_mix_int | ||
| ) |
Toroidal-poloidal Fourier filter for the regions 1 and 2 This version of the filter is parallelized to a high degree for optimal performance, and allows for multiple toroidal mode numbers. Removes high poloidal mode numbers from flux-surfaces while retaining small scale poloidal variations close to the divertor plates. This is achieved by applying a window function that removes the near-divertor part from the data. The windowed data is then low-pass filtered and the high-m variations are removed by calculating x_filtered = (1-win)*x - win*x_filtered.
Additionally, only one toroidal mode number is kept.
NOTE: WINDOW HAS NOT BEEN IMPLEMENTED YET —> USING WIN=1
- Parameters
-
[in] grid grid data, type(grid_type) [in] nphi number of toroidal grid points, integer [in] ntor_min minimal numerical toroidal mode number, integer [in] ntor_max maximal numerical toroidal mode number, integer [in] ntor_min_real minimal real (incl. wedge factor) toroidal mode number, integer [in] ntor_max_real maximal real (incl. wedge factor) toroidal mode number, integer [in] bands_on Whether to use only the main band of resonant modes or also side bands (n>sml_nphi_total/2), logical [in] mpol_min minimal poloidal mode number, integer [in] mpol_max maximal poloidal mode number, integer [in,out] x input data, real(8) [in] op_mode mode of operation (integer): 1) simple range of pol. mode numbers, 2) resonant pol. modes [in] num_mres_q number of poloidal modes retained around the res. mode divided by the safety factor in op_mode=2 [in] inpsi Inner filter boundary, real(8) [in] outpsi Outer filter boundary, real(8) [in] bd_width Boundary width, real(8) [in] div_mix Whether to blend unfiltered data near the divertor with filtered data (due to windowing function), logical
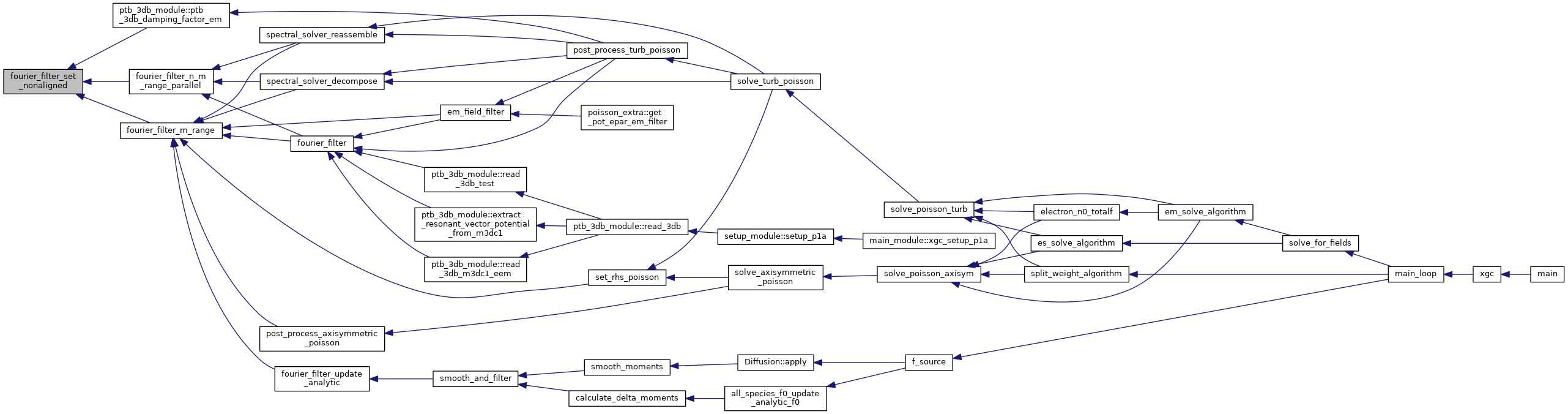
◆ fourier_filter_set_nonaligned()
| subroutine fourier_filter_set_nonaligned | ( | type(grid_type), intent(in) | grid, |
| real (kind=8), dimension(grid%nnode), intent(inout) | x | ||
| ) |
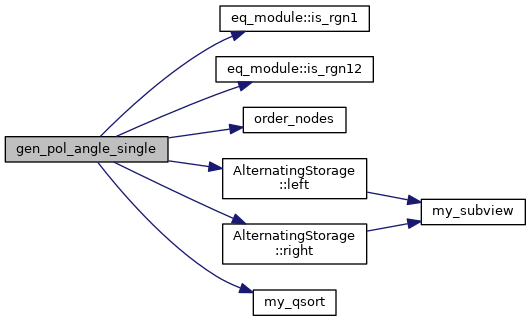
◆ gen_pol_angle_single()
| subroutine calc_gen_theta_psi::gen_pol_angle_single | ( | integer, intent(in) | i | ) |

◆ get_b_and_derivs_cyl()
| subroutine get_b_and_derivs_cyl | ( | real(kind=8), intent(in) | r, |
| real(kind=8), intent(in) | z, | ||
| real(kind=8), intent(out) | B_mag, | ||
| real(kind=8), intent(out) | br, | ||
| real(kind=8), intent(out) | bphi, | ||
| real(kind=8), intent(out) | bz, | ||
| real(kind=8), intent(out) | dbrdr, | ||
| real(kind=8), intent(out) | dbpdr, | ||
| real(kind=8), intent(out) | dbzdr, | ||
| real(kind=8), intent(out) | dbrdp, | ||
| real(kind=8), intent(out) | dbpdp, | ||
| real(kind=8), intent(out) | dbzdp, | ||
| real(kind=8), intent(out) | dbrdz, | ||
| real(kind=8), intent(out) | dbpdz, | ||
| real(kind=8), intent(out) | dbzdz | ||
| ) |


◆ get_pe_info()
| subroutine get_pe_info | ( | integer | mype, |
| integer | totalpe | ||
| ) |
◆ order_nodes()
| subroutine calc_gen_theta_psi::order_nodes | ( | type(grid_type), intent(in) | grid, |
| integer, intent(in) | isurf, | ||
| integer, intent(in) | isize, | ||
| integer, intent(in) | idx_start, | ||
| real (kind=8), dimension(isize), intent(out) | theta, | ||
| integer, dimension(isize), intent(out) | idx | ||
| ) |
Sorts input SOL flux-surface according to the poloidal arclength l_theta where l_theta=0 at the outer midplane.
- Parameters
-
[in] grid grid data; type(grid_type) [in] isurf flux-surface index; integer [in] isize length of the flux-surface; integer @apram[out] theta output arclength; real(8) [out] idx output sort index; integer

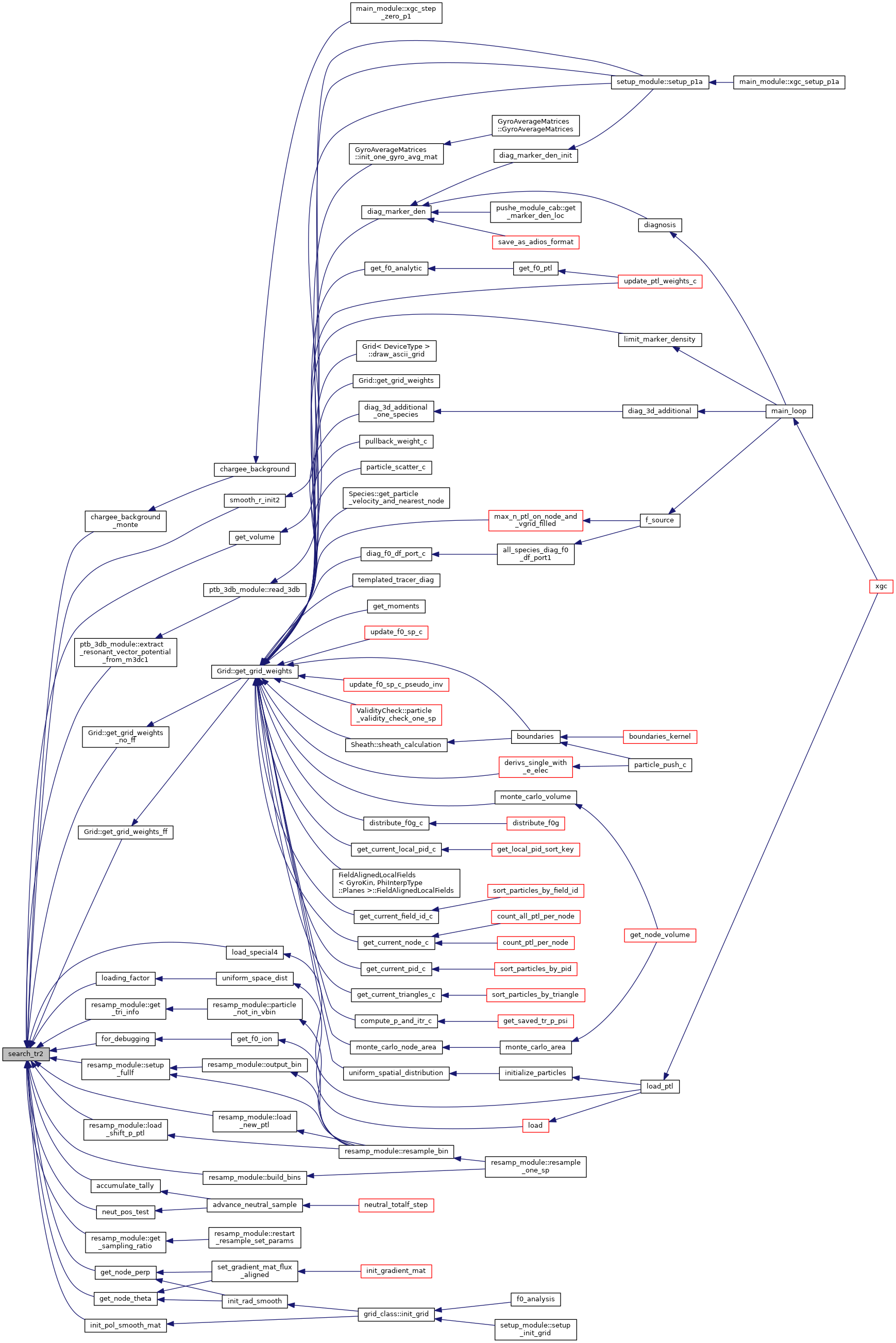
◆ search_tr2()
| subroutine search_tr2 | ( | type(grid_type) | grid, |
| real(kind=8), dimension(2) | xy, | ||
| integer | itr, | ||
| real(kind=8), dimension(3) | p | ||
| ) |
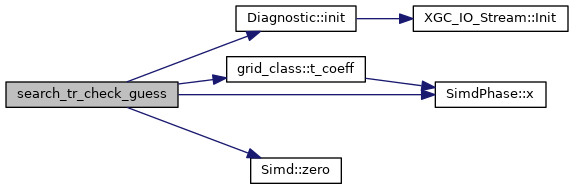
◆ search_tr_check_guess()
| subroutine search_tr_check_guess | ( | type(grid_type), intent(in) | grid, |
| real (kind=8), dimension(2), intent(in) | x, | ||
| integer, intent(in) | init, | ||
| integer, intent(out) | itr, | ||
| real (kind=8), dimension(3), intent(out) | p | ||
| ) |

◆ write_gradient_mat()
| subroutine write_gradient_mat | ( | type (grid_type), intent(inout) | grid | ) |