es_poisson.F90 File Reference

#include "petsc_v3_10_defs.h"
#include <petsc/finclude/petsc.h>

Include dependency graph for es_poisson.F90:

Data Types
interface	f90moduleinterfaces::pcsetapplicationcontext
interface	f90moduleinterfaces::pcgetapplicationcontext

Modules
module	f90moduleinterfaces

Macros
#define	XGC1   1

Functions/Subroutines
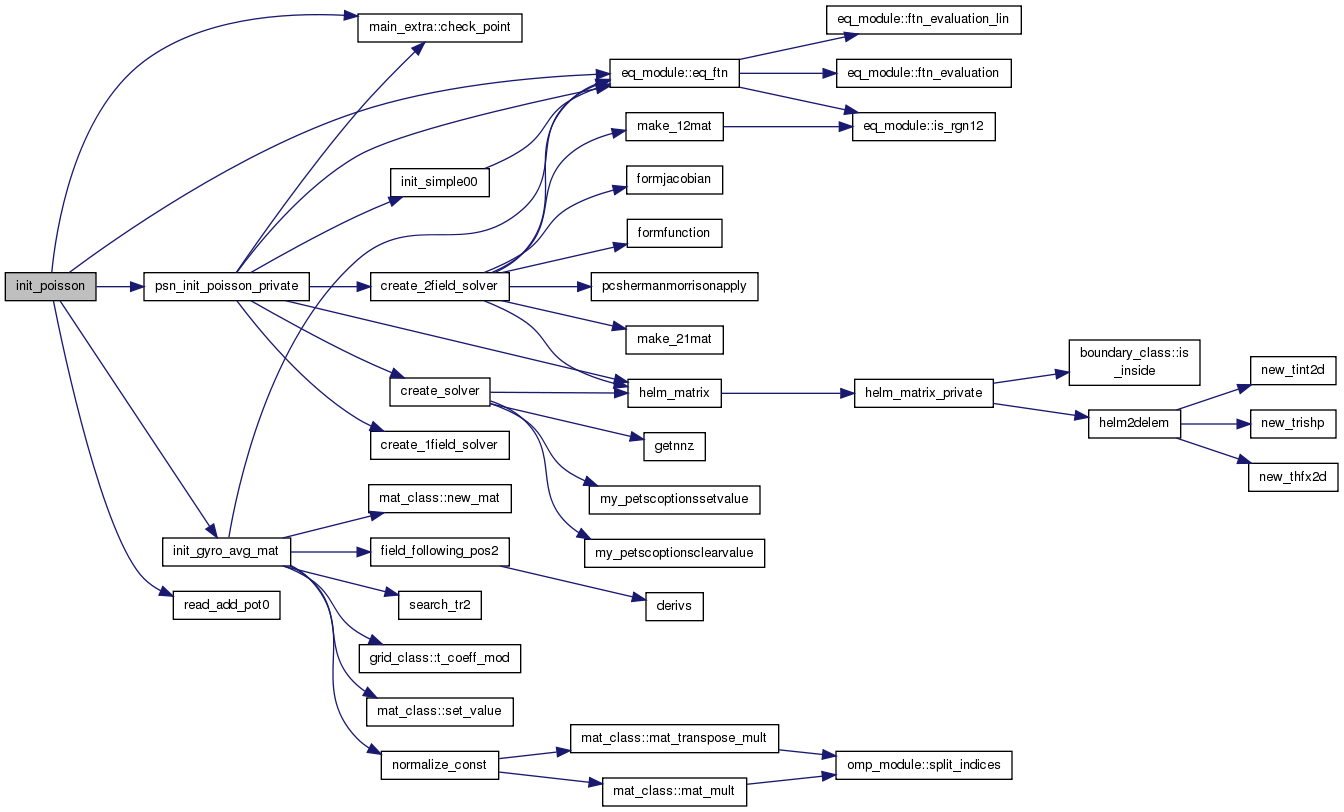
subroutine	init_poisson (grid, psn, iflag_dummy)
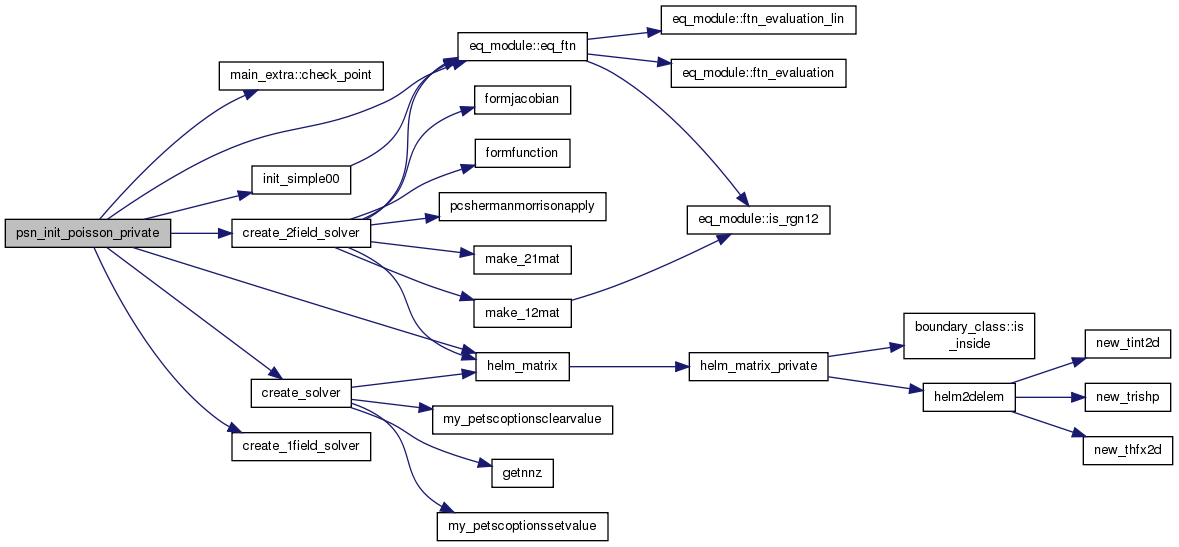
subroutine	psn_init_poisson_private (psn, grid, nrhs)
subroutine	pcshermanmorrisonapply (pc, xin, yout, ierr)
subroutine	getnnz (grid, nloc, low, high, d_nnz, o_nnz, xgc_petsc, nglobal, ierr)
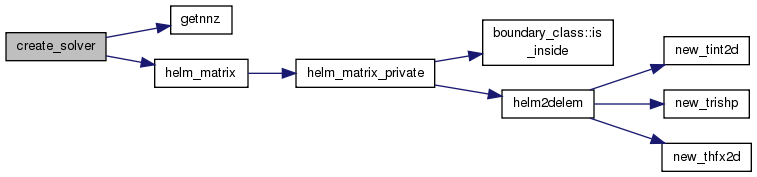
subroutine	create_solver (this, grid, bc, ierr)
subroutine	create_1field_solver (grid, solver)
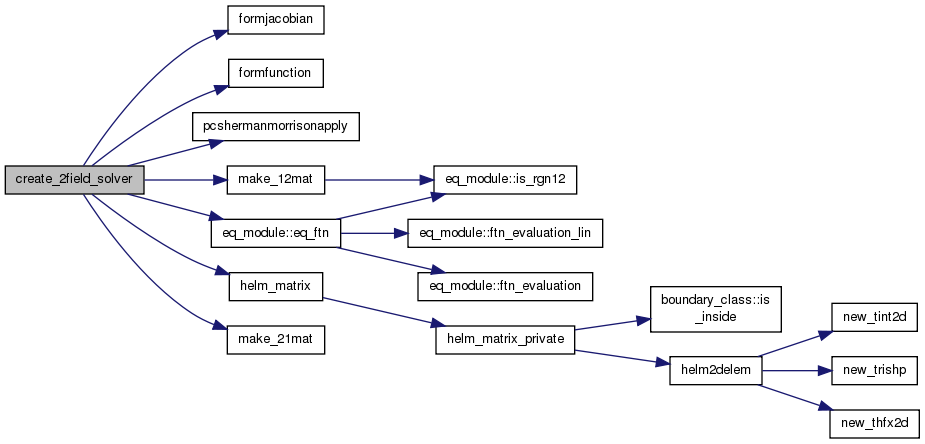
subroutine	create_2field_solver (grid, bd, solver)
subroutine	make_12mat (grid, Bmat, BIdentMat, FSAMass_Te, solver, bd, scale, xgc_petsc)
subroutine	make_21mat (grid, Cmat, Bmat, CConstBCVec, bd, xgc_petsc)
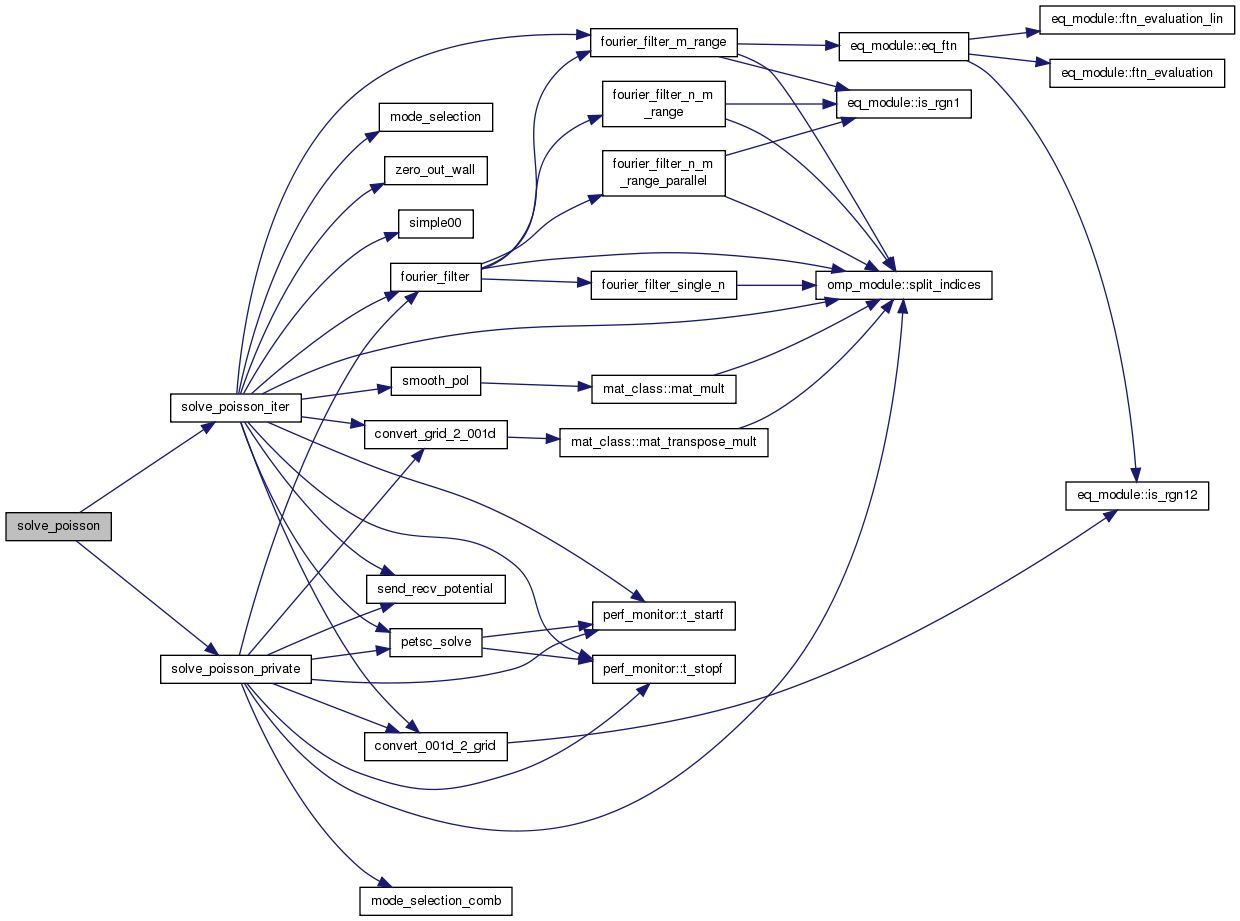
subroutine	solve_poisson (grid, psn, iflag)
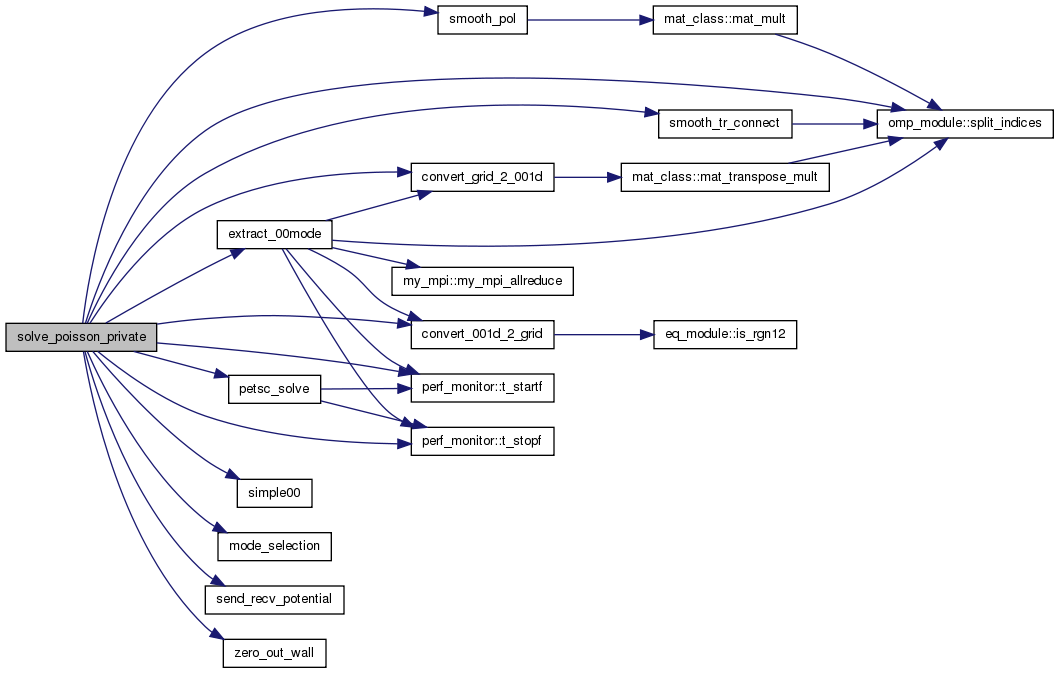
subroutine	solve_poisson_private (grid, psn, iflag)
subroutine	zero_out_wall (var)
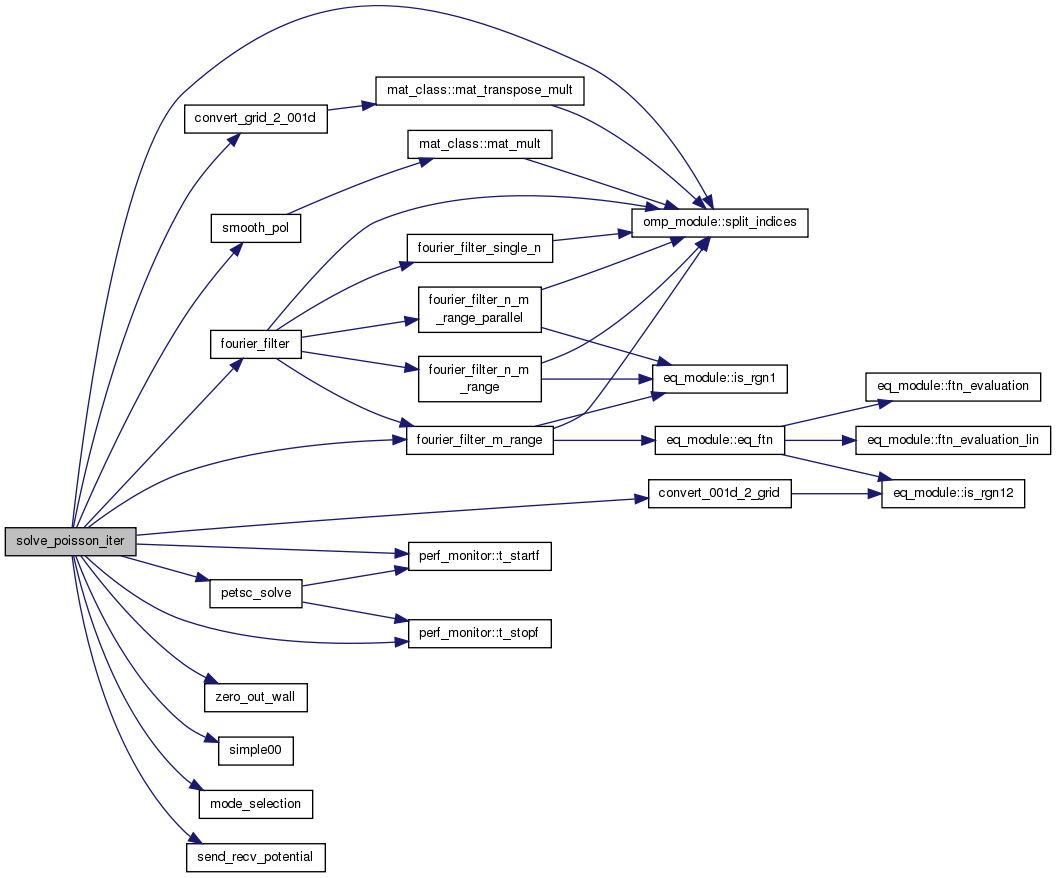
subroutine	solve_poisson_iter (grid, psn, iflag)
	Poisson solver that uses an iterative method to solve for the axisymmetric electrostatic potential: The Poisson equation for the axisymmetric mode is \(-\nabla_\perp \cdot \xi \nabla_\perp \overline{\phi}_{k+1} + \frac{e n_0/T_{e,0}} \overline{\phi}_{k+1} = e \left( \langle \overline{\delta n_i} \rangle_g - \overline{\delta n_{e,NA}} \right) + \frac{e n_0/T_{e,0}} \langle \phi_{k} \rangle_{fs} \) where \(k\) is the iteration index, \(xi\) is the electric susceptibility, \(e\) is the elementary charge, \(n_0\) and \(T_0\) are the background density and temperature, \(\langle \overline{\delta n_i} \rangle_g\) is the gyroaveraged ion (gyrocenter) charge density, \(\overline{\delta n_{e,NA}}\) is the non-adiabatic electron charge density, and \(\langle\dots\rangle\) is the the flux-surface average. \(\overline{\dots}\) is the toroidal average. More...

Macro Definition Documentation

XGC1

#define XGC1   1

Function/Subroutine Documentation

create_1field_solver()

subroutine create_1field_solver	(	type(grid_type)	grid,
		type(xgc_solver)	solver
	)

create_2field_solver()

subroutine create_2field_solver	(	type(grid_type)	grid,
		type(boundary2_type)	bd,
		type(xgc_solver)	solver
	)

Here is the call graph for this function:

Here is the caller graph for this function:

create_solver()

subroutine create_solver	(	type(xgc_solver)	this,
		type(grid_type), intent(in)	grid,
		type(boundary2_type), intent(in)	bc,
			ierr
	)

Here is the call graph for this function:

getnnz()

subroutine getnnz	(	type(grid_type), intent(in)	grid,
			nloc,
			low,
			high,
			d_nnz,
			o_nnz,
		dimension(grid%nnode), intent(in)	xgc_petsc,
			nglobal,
			ierr
	)

init_poisson()

subroutine init_poisson	(	type(grid_type)	grid,
		type(psn_type)	psn,
		integer	iflag_dummy
	)

Here is the call graph for this function:

make_12mat()

subroutine make_12mat	(	type(grid_type)	grid,
		intent(out)	Bmat,
			BIdentMat,
		intent(in)	FSAMass_Te,
		type(xgc_solver)	solver,
		type(boundary2_type), intent(in)	bd,
		real (8), intent(in)	scale,
		dimension(grid%nnode), intent(in)	xgc_petsc
	)

Here is the call graph for this function:

Here is the caller graph for this function:

make_21mat()

subroutine make_21mat	(	type(grid_type)	grid,
			Cmat,
		intent(in)	Bmat,
			CConstBCVec,
		type(boundary2_type), intent(in)	bd,
		dimension(grid%nnode), intent(in)	xgc_petsc
	)

Here is the caller graph for this function:

pcshermanmorrisonapply()

subroutine pcshermanmorrisonapply	(		pc,
			xin,
			yout,
			ierr
	)

Here is the caller graph for this function:

psn_init_poisson_private()

subroutine psn_init_poisson_private	(	type(psn_type)	psn,
		type(grid_type)	grid,
		integer	nrhs
	)

Here is the call graph for this function:

Here is the caller graph for this function:

solve_poisson()

subroutine solve_poisson	(	type(grid_type)	grid,
		type(psn_type)	psn,
		integer, intent(in)	iflag
	)

Here is the call graph for this function:

solve_poisson_iter()

subroutine solve_poisson_iter	(	type(grid_type)	grid,
		type(psn_type)	psn,
		integer, intent(in)	iflag
	)

Poisson solver that uses an iterative method to solve for the axisymmetric electrostatic potential: The Poisson equation for the axisymmetric mode is \(-\nabla_\perp \cdot \xi \nabla_\perp \overline{\phi}_{k+1} + \frac{e n_0/T_{e,0}} \overline{\phi}_{k+1} = e \left( \langle \overline{\delta n_i} \rangle_g - \overline{\delta n_{e,NA}} \right) + \frac{e n_0/T_{e,0}} \langle \phi_{k} \rangle_{fs} \) where \(k\) is the iteration index, \(xi\) is the electric susceptibility, \(e\) is the elementary charge, \(n_0\) and \(T_0\) are the background density and temperature, \(\langle \overline{\delta n_i} \rangle_g\) is the gyroaveraged ion (gyrocenter) charge density, \(\overline{\delta n_{e,NA}}\) is the non-adiabatic electron charge density, and \(\langle\dots\rangle\) is the the flux-surface average. \(\overline{\dots}\) is the toroidal average.

The non-axisymmetric Poisson equation is simpler:

Here is the call graph for this function:

Here is the caller graph for this function:

solve_poisson_private()

subroutine solve_poisson_private	(	type(grid_type)	grid,
		type(psn_type)	psn,
		integer, intent(in)	iflag
	)

Here is the call graph for this function:

zero_out_wall()

subroutine solve_poisson_private::zero_out_wall

(

real (8), dimension(grid%nnode), intent(inout)

var

)