Data Types
type	col_f_module::col_f_core_type

Modules
module	col_f_module

Functions/Subroutines
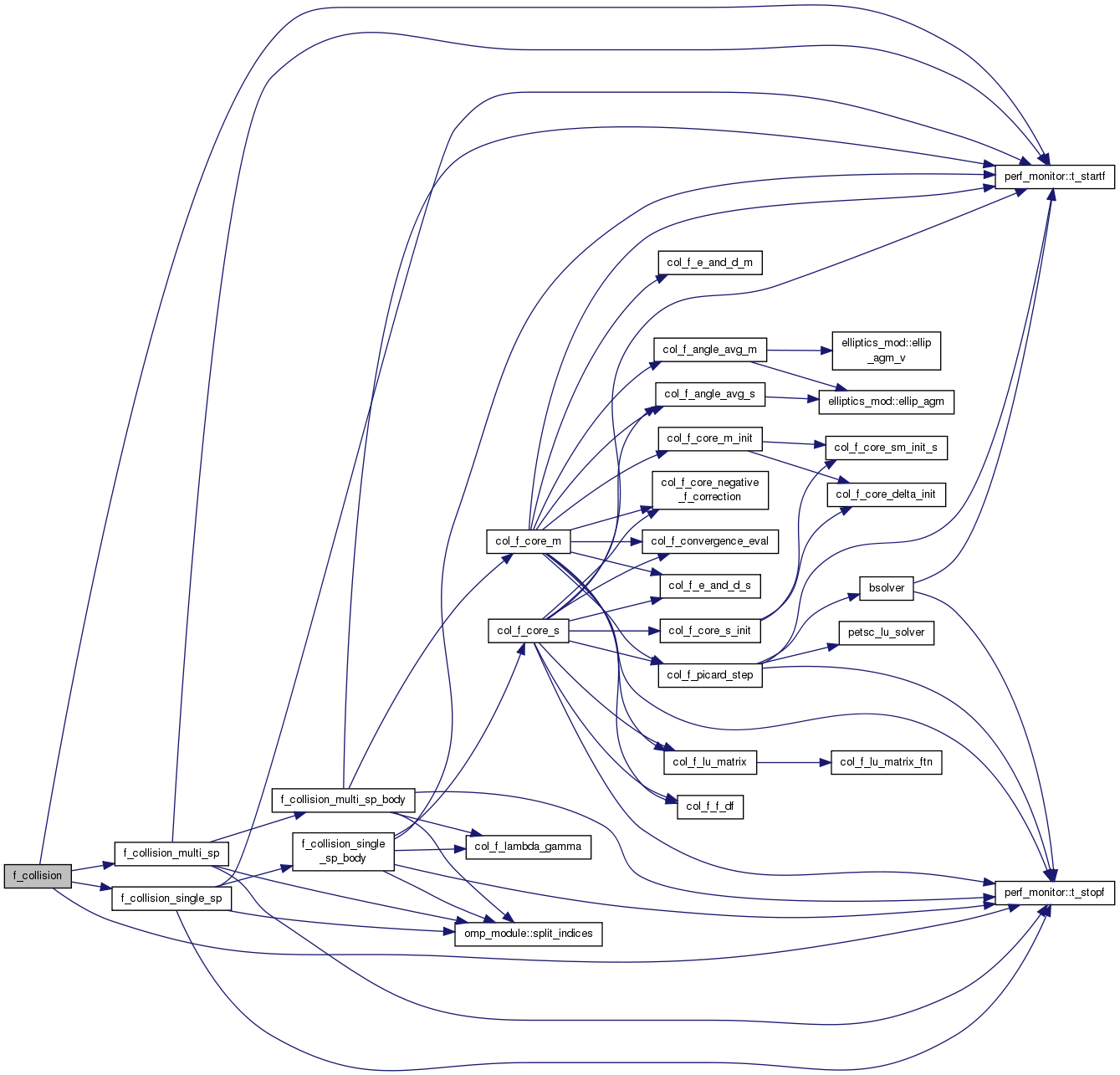
subroutine	f_collision (grid)

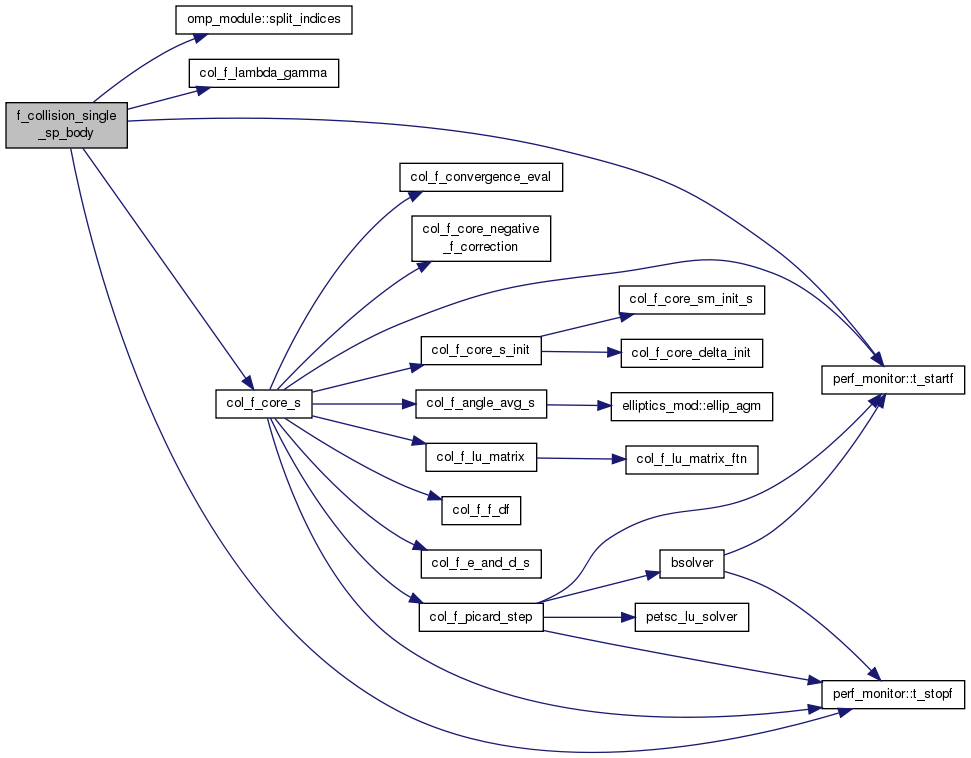
subroutine	f_collision_single_sp_body (node_in, grid, st, df, col_f_mat, col_f_ksp, col_f_vecb, col_f_vecx, converged)

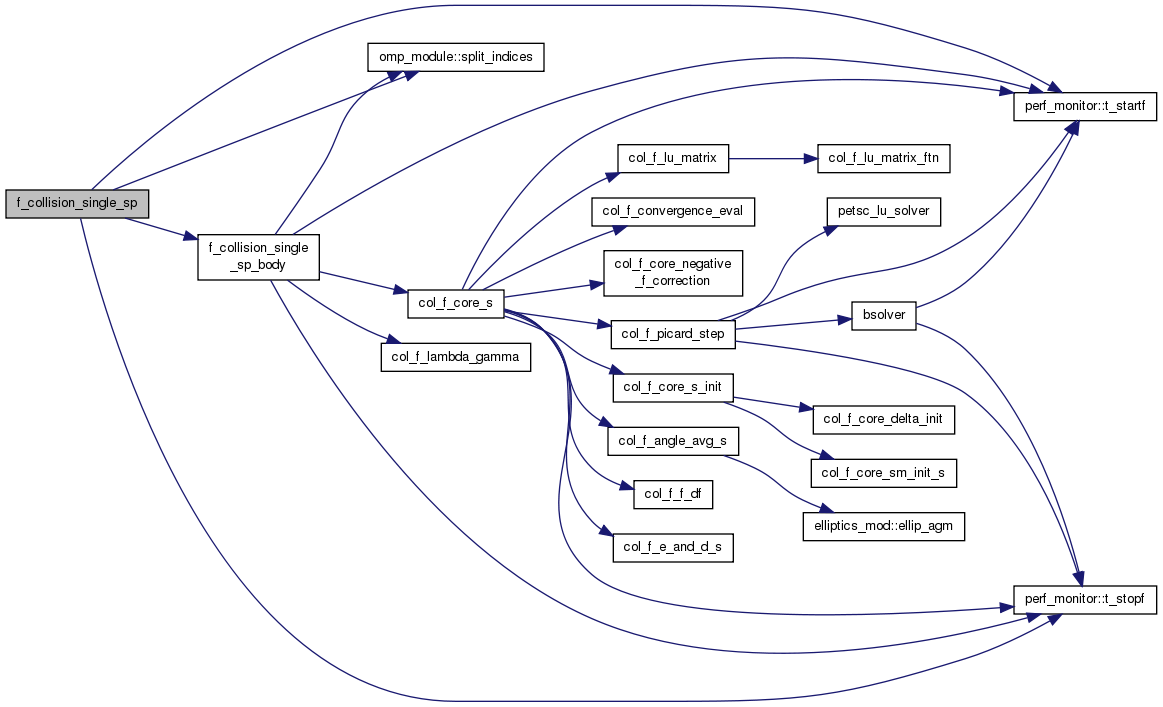
subroutine	f_collision_single_sp (grid, st)

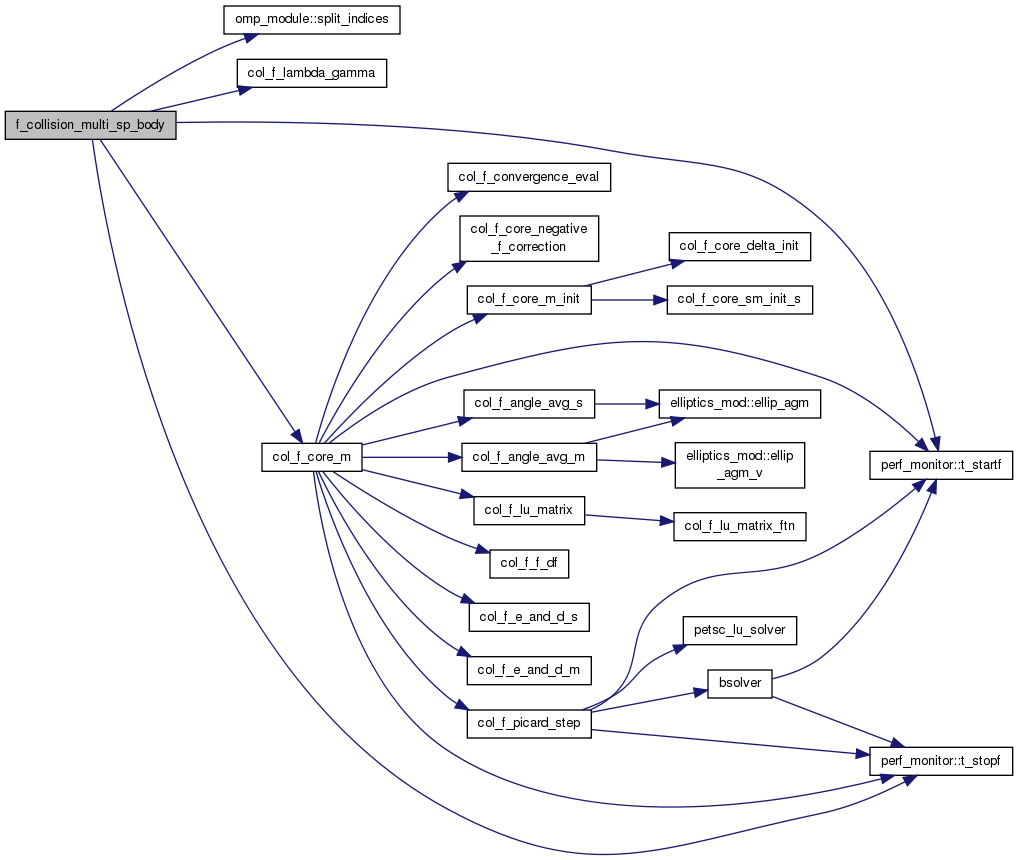
subroutine	f_collision_multi_sp_body (node_in, grid, st0, st1, df, col_f_mat, col_f_ksp, col_f_vecb, col_f_vecx, converged)

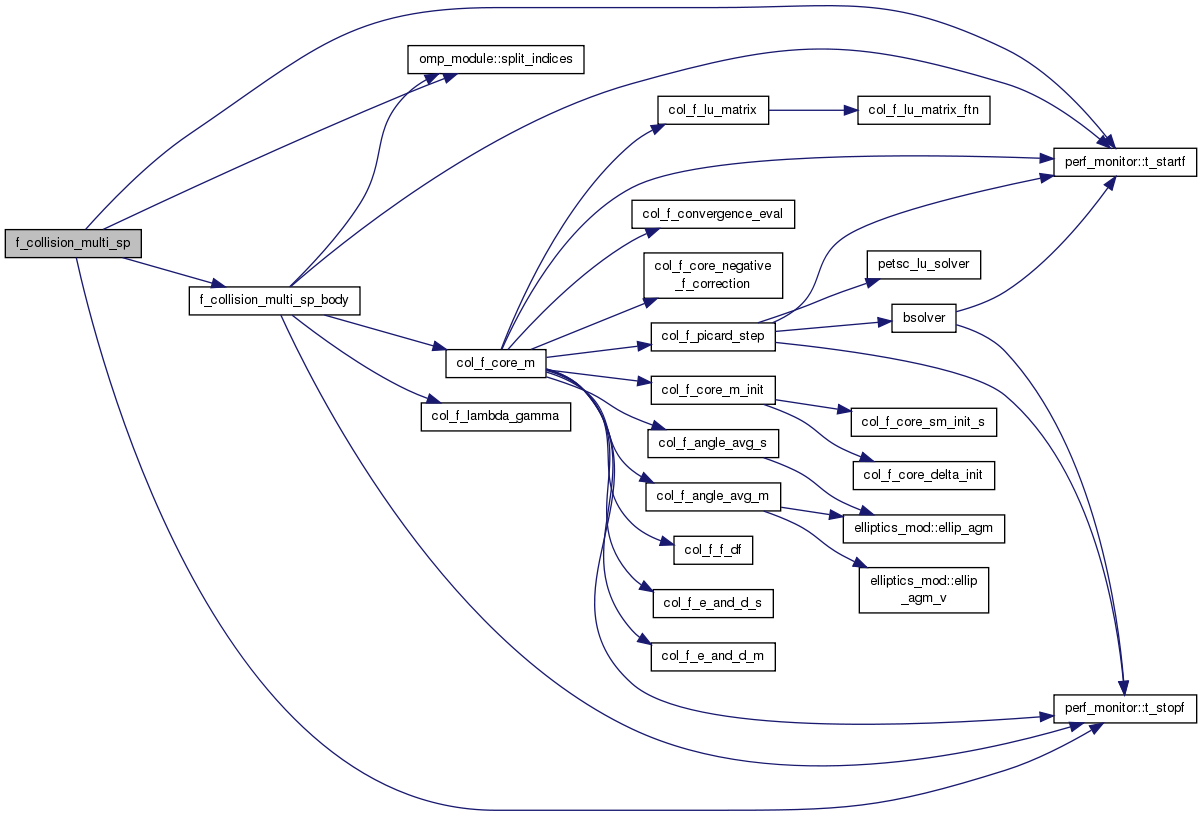
subroutine	f_collision_multi_sp (grid, st0, st1)

subroutine	gather_df0g (isize, i_beg, i_end)

subroutine	col_f_lambda_gamma (den, ti_ev, te_ev, massi, masse, gammac)

subroutine	col_f_core_s (st, Dlx, mesh_dr, mesh_dz, dist_n, vol, vpic_gamma, df, node, vpic_ierr, col_f_mat, col_f_ksp, col_f_vecb, col_f_vecx, converged)

subroutine	col_f_core_s_init (st, cs, dist_n, mesh_dr, mesh_dz, dlx, vol, node)

subroutine	col_f_core_m_init (sti, ci, dist_ni, mesh_dri, mesh_dzi, dlxi, voli, ste, ce, dist_ne, mesh_dre, mesh_dze, dlxe, vole, node)

subroutine	col_f_core_sm_init_s (cs, mass, mesh_dr, mesh_dz, dlx, vol)

subroutine	col_f_core_delta_init (cs, node)

subroutine	col_f_f_df (cs, op_mode, f, f_half, dfdr, dfdz)

subroutine	col_f_core_m (sti, Dlxi, mesh_dri, mesh_dzi, dist_ni, voli, ste, Dlxe, mesh_dre, mesh_dze, dist_ne, vole, vpic_gamma, dfi, dfe, node, vpic_ierr, col_f_mat, col_f_ksp, col_f_vecb, col_f_vecx, converged)

subroutine	col_f_setup

subroutine	col_f_petsc_initialize (col_f_mat, col_f_vecb, col_f_vecx, col_f_ksp)

subroutine	col_f_core_negative_f_correction (f_new, vpar_all, vperp_all, vol_all, npar, nperp, mass, n0, u0, T0, tile_size_max, negative_count, correction_error)
	Smoothing routine to correct negative values in the distribution function after collisions while conserving mass, momentum and energy as far as possible. First, the velocity space is divided into quadratic tiles (allowed tile sizes are determined automatically). If more than one tile size is allowed, the routine loops over all tile sizes starting from the smallest one until an exit condition is met (see below). Inside the loop over tile sizes –> The routine loops over all tiles and checks each tile for negative values. If no negative values are found, the tile is not modified. If negative values are found, this routine minimizes the sum (over the tile) of the quadratic deviation from a shifted Maxwellian (for the density, temperature and flow of the input distribution function) with the constraints of mass, momentum and density conservation, and positivity of f. This is done with quadratic programming using the Active-Set-Method algorithm by Goldfarb/Idnani (1983). If all negative values have been removed by this optimization and the relative errors of mass, momentum and energy are smaller than 1E-7, the loop over tile sizes is interrupted. If there are negative values left, the routine proceeds to the next tile size. In case there are still negative values left at the largest allowed tile size, negative values on a tile are set to 1% of the corresponding shifted Maxwellian and all positive values are shifted such as to conserve at least the total mass of the tile. (If this shift would make a positive value on a tile negative, the accuracy of mass conservation is limited!) More...

Variables
integer	col_f_module::col_f_nthreads

integer	col_f_module::col_f_nvr

integer	col_f_module::col_f_nvz

integer	col_f_module::col_f_ntotal_v

real(kind=8)	col_f_module::col_f_dt

integer, dimension(:,:), allocatable	col_f_module::index_map_lu

integer, dimension(:), allocatable	col_f_module::lu_cvalues

integer, dimension(:), allocatable	col_f_module::lu_rowindx

integer, dimension(:), allocatable	col_f_module::lu_colptr

integer	col_f_module::lu_n

integer	col_f_module::lu_nnz

integer	col_f_module::lu_nrhs

integer	col_f_module::lu_ldb

integer, parameter	col_f_module::col_f_tile_size_max =5

real(kind=8), parameter	col_f_module::col_f_tol_negative =0.1D0

integer, parameter, private	col_f_module::max_threads =32

logical, parameter	col_f_module::use_superlu = .false.

integer, dimension(max_threads)	col_f_module::col_f_mat_list

integer, dimension(max_threads)	col_f_module::col_f_vecb_list

integer, dimension(max_threads)	col_f_module::col_f_vecx_list

integer, dimension(max_threads)	col_f_module::col_f_ksp_list

Function/Subroutine Documentation

◆ col_f_core_delta_init()

subroutine col_f_core_delta_init	(	type(col_f_core_type), intent(inout)	cs,
		integer, intent(in)	node
	)

Here is the caller graph for this function:

◆ col_f_core_m()

subroutine col_f_core_m	(	integer, intent(in)	sti,
		real (kind=8)	Dlxi,
		real (kind=8)	mesh_dri,
		real (kind=8)	mesh_dzi,
		real (kind=8), dimension(col_f_nvr, col_f_nvz)	dist_ni,
		real (kind=8), dimension(1:col_f_nvr)	voli,
		integer, intent(in)	ste,
		real (kind=8)	Dlxe,
		real (kind=8)	mesh_dre,
		real (kind=8)	mesh_dze,
		real (kind=8), dimension(col_f_nvr, col_f_nvz)	dist_ne,
		real (kind=8), dimension(1:col_f_nvr)	vole,
		real (kind=8), dimension(4)	vpic_gamma,
		real (kind=8), dimension(col_f_nvr, col_f_nvz)	dfi,
		real (kind=8), dimension(col_f_nvr, col_f_nvz)	dfe,
		integer, intent(in)	node,
		integer	vpic_ierr,
		integer	col_f_mat,
		integer	col_f_ksp,
		integer	col_f_vecb,
		integer	col_f_vecx,
		integer, intent(inout)	converged
	)

Here is the call graph for this function:

Here is the caller graph for this function:

◆ col_f_core_m_init()

subroutine col_f_core_m_init	(	integer, intent(in)	sti,
		type(col_f_core_type), intent(inout)	ci,
		real (kind=8), dimension(col_f_nvr, col_f_nvz), intent(in)	dist_ni,
		real (8), intent(in)	mesh_dri,
		real (8), intent(in)	mesh_dzi,
		real (8), intent(in)	dlxi,
		real (kind=8), dimension(1:col_f_nvr), intent(in)	voli,
		integer, intent(in)	ste,
		type(col_f_core_type), intent(inout)	ce,
		real (kind=8), dimension(col_f_nvr, col_f_nvz), intent(in)	dist_ne,
		real (8), intent(in)	mesh_dre,
		real (8), intent(in)	mesh_dze,
		real (8), intent(in)	dlxe,
		real (kind=8), dimension(1:col_f_nvr), intent(in)	vole,
		integer, intent(in)	node
	)

Here is the call graph for this function:

Here is the caller graph for this function:

◆ col_f_core_negative_f_correction()

subroutine col_f_core_negative_f_correction	(	real (kind=8), dimension(nperp,npar), intent(inout)	f_new,
		real (kind=8), dimension(npar), intent(in)	vpar_all,
		real (kind=8), dimension(nperp), intent(in)	vperp_all,
		real (kind=8), dimension(nperp), intent(in)	vol_all,
		integer, intent(in)	npar,
		integer, intent(in)	nperp,
		real (kind=8), intent(in)	mass,
		real (kind=8), intent(in)	n0,
		real (kind=8), intent(in)	u0,
		real (kind=8), intent(in)	T0,
		integer, intent(in)	tile_size_max,
		real (kind=8), intent(out)	negative_count,
		real (kind=8), dimension(3), intent(out)	correction_error
	)

Smoothing routine to correct negative values in the distribution function after collisions while conserving mass, momentum and energy as far as possible. First, the velocity space is divided into quadratic tiles (allowed tile sizes are determined automatically). If more than one tile size is allowed, the routine loops over all tile sizes starting from the smallest one until an exit condition is met (see below). Inside the loop over tile sizes –> The routine loops over all tiles and checks each tile for negative values. If no negative values are found, the tile is not modified. If negative values are found, this routine minimizes the sum (over the tile) of the quadratic deviation from a shifted Maxwellian (for the density, temperature and flow of the input distribution function) with the constraints of mass, momentum and density conservation, and positivity of f. This is done with quadratic programming using the Active-Set-Method algorithm by Goldfarb/Idnani (1983). If all negative values have been removed by this optimization and the relative errors of mass, momentum and energy are smaller than 1E-7, the loop over tile sizes is interrupted. If there are negative values left, the routine proceeds to the next tile size. In case there are still negative values left at the largest allowed tile size, negative values on a tile are set to 1% of the corresponding shifted Maxwellian and all positive values are shifted such as to conserve at least the total mass of the tile. (If this shift would make a positive value on a tile negative, the accuracy of mass conservation is limited!)

Minimization process Minimize sum_i[f_i - f_(M,i)]^2 on each tile with negative values f_i —> Minimize: 1/2 * x^T.Q.x - d^T.x where : A_1^T.x = b_1 (Equality constraints –> mass, momentum, energy) a_2^T.x >= b_2 (Inequality constraints –> positivity of f) Q is diagonal –> Q = 2*I d^T = +2*f_M A_1^T = | dV1 dV2 ... | | vpar1*dV1 vpar2*dV2 ... | | v_1^2*dV1 v_2^2*dV2 ... | A_2^T = I b_1^T = (n0,p0,E0) (–> mass, momentum, density) b_2^T = (0,0,...,0) (–> positivity)

Since Q is diagonal, it is trivial to factorize it into Q = R^T.R –> R^T = R = sqrt(2)*I Then we pass only R^-1 = 1/sqrt(2)*I to the solver

Parameters

[in,out]	f_new	Distribution function to be smoothed, real(8)
[in]	vpar_all	Parallel velocity grid, real(8)
[in]	vperp_all	Perp. velocity grid, real(8)
[in]	vol_all	Volume elements (d^3v = 2pi v_perp dv_perp dv_par, real(8)
[in]	npar	Par. vel. grid size, integer
[in]	nperp	Perp. vel. grid size, integer
[in]	mass	Species mass, real(8)
[in]	n0	Density moment of f_new, real(8)
[in]	u0	Momentum density (!!!) moment of f_new, real(8)
[in]	T0	Temperature moment of f_new, real(8)
[in]	tile_size_max	Maximal tile size for smoothing, integer
[out]	negative_count	Number of negative values left after optimization
[out]	correction_error	Relative error of mass, momentum, energy on exit, real(8)

Here is the caller graph for this function:

◆ col_f_core_s()

subroutine col_f_core_s	(	integer	st,
		real (kind=8)	Dlx,
		real (kind=8)	mesh_dr,
		real (kind=8)	mesh_dz,
		real (kind=8), dimension(col_f_nvr, col_f_nvz)	dist_n,
		real (kind=8), dimension(1:col_f_nvr)	vol,
		real (kind=8)	vpic_gamma,
		real (kind=8), dimension(col_f_nvr, col_f_nvz)	df,
		integer, intent(in)	node,
		integer	vpic_ierr,
		integer	col_f_mat,
		integer	col_f_ksp,
		integer	col_f_vecb,
		integer	col_f_vecx,
		integer, intent(inout)	converged
	)

Here is the call graph for this function:

Here is the caller graph for this function:

◆ col_f_core_s_init()

subroutine col_f_core_s_init	(	integer, intent(in)	st,
		type(col_f_core_type), intent(inout)	cs,
		real (kind=8), dimension(col_f_nvr, col_f_nvz), intent(in)	dist_n,
		real (8), intent(in)	mesh_dr,
		real (8), intent(in)	mesh_dz,
		real (8), intent(in)	dlx,
		real (kind=8), dimension(1:col_f_nvr), intent(in)	vol,
		integer, intent(in)	node
	)

Here is the call graph for this function:

Here is the caller graph for this function:

◆ col_f_core_sm_init_s()

subroutine col_f_core_sm_init_s	(	type(col_f_core_type)	cs,
		real (kind=8)	mass,
		real (kind=8)	mesh_dr,
		real (kind=8)	mesh_dz,
		real (kind=8)	dlx,
		real (kind=8), dimension(1:col_f_nvr)	vol
	)

Here is the caller graph for this function:

◆ col_f_f_df()

subroutine col_f_f_df	(	type(col_f_core_type), intent(in)	cs,
		integer, intent(in)	op_mode,
		real(kind=8), dimension(col_f_nvr, col_f_nvz)	f,
		real(kind=8), dimension(col_f_nvr-1, col_f_nvz-1)	f_half,
		real(kind=8), dimension(col_f_nvr-1, col_f_nvz-1)	dfdr,
		real(kind=8), dimension(col_f_nvr-1, col_f_nvz-1)	dfdz
	)

Here is the caller graph for this function:

◆ col_f_lambda_gamma()

subroutine col_f_lambda_gamma	(	real (8), intent(in)	den,
		real (8), intent(in)	ti_ev,
		real (8), intent(in)	te_ev,
		real (8), intent(in)	massi,
		real (8), intent(in)	masse,
		real (8), dimension(4), intent(out)	gammac
	)

Here is the caller graph for this function:

◆ col_f_petsc_initialize()

subroutine col_f_setup::col_f_petsc_initialize	(	col_f_mat,
		col_f_vecb,
		col_f_vecx,
		col_f_ksp
	)

Here is the caller graph for this function:

◆ col_f_setup()

subroutine col_f_setup ( )

Here is the call graph for this function:

Here is the caller graph for this function:

◆ f_collision()

subroutine f_collision ( type(grid_type) grid )

Here is the call graph for this function:

Here is the caller graph for this function:

◆ f_collision_multi_sp()

subroutine f_collision_multi_sp	(	type(grid_type)	grid,
		integer, intent(in)	st0,
		integer, intent(in)	st1
	)

Here is the call graph for this function:

Here is the caller graph for this function:

◆ f_collision_multi_sp_body()

subroutine f_collision_multi_sp_body	(	integer, intent(in)	node_in,
		type(grid_type)	grid,
		integer, intent(in)	st0,
		integer, intent(in)	st1,
		real (8), dimension(0:f0_nmu,-f0_nvp:f0_nvp,st0:st1), intent(out)	df,
		integer	col_f_mat,
		integer	col_f_ksp,
		integer	col_f_vecb,
		integer	col_f_vecx,
		integer, intent(inout)	converged
	)

Here is the call graph for this function:

Here is the caller graph for this function:

◆ f_collision_single_sp()

subroutine f_collision_single_sp	(	type(grid_type)	grid,
		integer, intent(in)	st
	)

Here is the call graph for this function:

Here is the caller graph for this function:

◆ f_collision_single_sp_body()

subroutine f_collision_single_sp_body	(	integer, intent(in)	node_in,
		type(grid_type)	grid,
		integer, intent(in)	st,
		real (8), dimension(0:f0_nmu,-f0_nvp:f0_nvp), intent(out)	df,
		integer	col_f_mat,
		integer	col_f_ksp,
		integer	col_f_vecb,
		integer	col_f_vecx,
		integer, intent(inout)	converged
	)

Here is the call graph for this function:

Here is the caller graph for this function:

◆ gather_df0g()

subroutine gather_df0g	(	integer, intent(in)	isize,
		integer, dimension(isize), intent(in)	i_beg,
		integer, dimension(isize), intent(in)	i_end
	)

Data Types

Modules

Functions/Subroutines

Variables

Function/Subroutine Documentation

◆ col_f_core_delta_init()

◆ col_f_core_m()

◆ col_f_core_m_init()

◆ col_f_core_negative_f_correction()

◆ col_f_core_s()

◆ col_f_core_s_init()

◆ col_f_core_sm_init_s()

◆ col_f_f_df()

◆ col_f_lambda_gamma()

◆ col_f_petsc_initialize()

◆ col_f_setup()

◆ f_collision()

◆ f_collision_multi_sp()

◆ f_collision_multi_sp_body()

◆ f_collision_single_sp()

◆ f_collision_single_sp_body()

◆ gather_df0g()