#include "t_coeff_mod_macro.h"
#include "petsc_version_defs.h"
#include <petsc/finclude/petscts.h>

Include dependency graph for diffusion.F90:

Functions/Subroutines
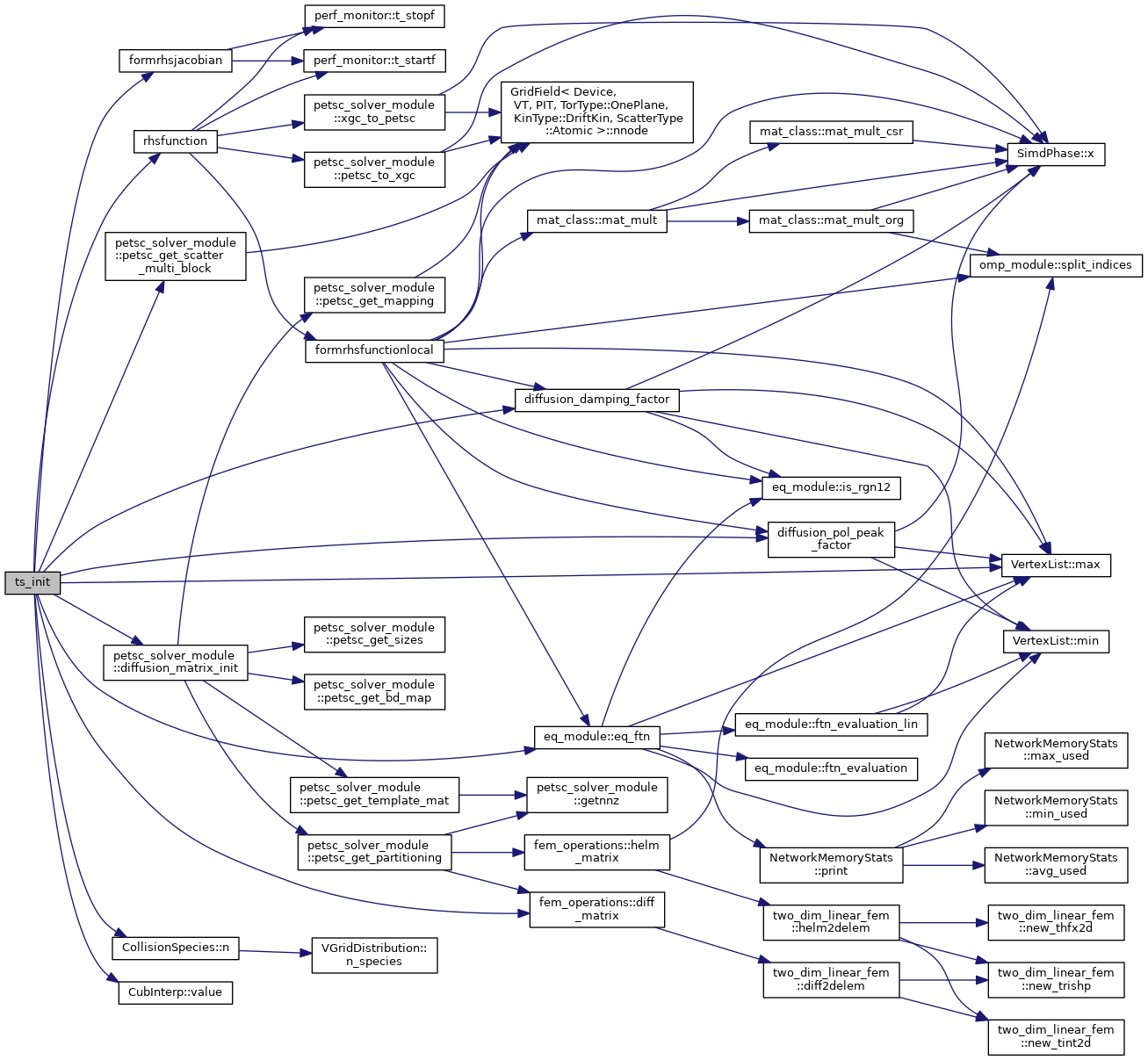
subroutine	ts_init (a_bc, a_ts, is_update)
	Initializes the PETSc time stepper for the 2D diffusion solver. This routine sets up a system of conserving Fick's law type equations on the 2D XGC solver mesh for: density, flow and parallel and perpendicular temperature, i.e., 3*n_species+1 equations. The linear terms of the form \(\nabla \cdot \boldsymbol{D}.\nabla X \) are discretized with linear finite elements. The nonlinear terms are discretized with finite difference. The diffusivity tensor is set up such that only trnasport perpendicular to flux-surfaces is computed by this model. More...

real(kind=8) function	diffusion_damping_factor (x, psi)
	Calculates the damping factor for the diffusion coefficients and pinch velocity. More...

real(kind=8) function	diffusion_pol_peak_factor (x)
	Calculates the poloidal envelope of the anomalous transport By default, anomalous transport is a flux-function similar to 1D transport models. A ballooning structure can be added through the ballooning angle and the ballooning factor. More...

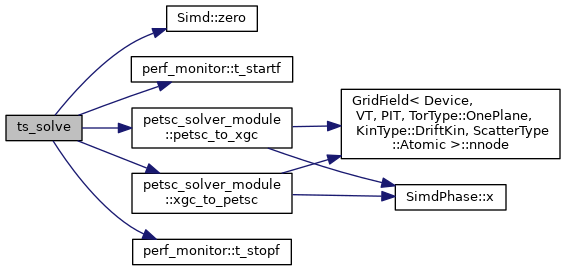
subroutine	ts_solve (a_ts, a_dt, XX_in, blocksize)
	This routine performs the actual time integration of the 2D diffusion model. More...

subroutine	formrhsjacobian (ts, t_dummy, a_XX, J, Jpre, a_ts, ierr)
	Update the RHS Jacobian In case the RHS Jacobian has any time dependent terms, this routine would compute the time dependent terms and put them into the final Jacobian for the present stage/step. More...

subroutine	formrhsjacobianlocal (a_ts, Jpre, XX_in, nn, ierr)
	Helper routine in XGC space for setting up the non-linear terms of the RHS Jacobian. This routine is used to compute any time dependent terms on the XGC solver grid. The result of this calculation will be inserted in the final RHS Jacobian. More...

subroutine	rhsfunction (ts, time, a_XX, a_FF, a_ts, ierr)
	Evaluates the RHS equation. More...

subroutine	formrhsfunctionlocal (a_ts, time, ts_it, snes_it, XX_in, div_gamma_in, rhs_out, nn)
	Computations in XGC space for RHS evaluation This includes 4 nonlinear terms for each species, one in the momentum equation, and three in the temperature equation. The terms are: (1/n) grad(n).(D+eta).grad(u) = (1/n) (D+eta) (dn/dr)(du/dr) in the momentum equation, and (T/n) div(D.grad(n)) = (T/n) d(D dn/dr)/dr (1/3n) grad(n).(5D+2chi).grad(T) = (5D+2chi)/(3n) (dn/dr)(dT/dr) (2m/3) grad(u).eta.grad(u) = (2m eta)/3 (du/dr)^2 Since this involves only radial gradients, we can simply use the XGC matrix gridgradientx. We have to take care, though, that vertices with undefined grad(psi) do not contribute (since we defined the tensor diffusivity to be D_ij=D(psi) psi_hat psi_hat). More...

subroutine	diffusion_solve (nn, XX_in, dt)

subroutine	initialize_diffusion (bd, is_update)

subroutine	update_diffusion_eq_ftn (n_species, npsi_in, psi_in, diff_coeff_in)

Function/Subroutine Documentation

real(kind=8) function diffusion_damping_factor	(	real (kind=8), dimension(2), intent(in)	x,
		real (kind=8), intent(in)	psi
	)

Calculates the damping factor for the diffusion coefficients and pinch velocity.

Parameters

[in]	x	Input (R,Z) coordinates, real(8)
[in]	psi	Input poloidal magnetic flux, real(8)

Here is the call graph for this function:

Here is the caller graph for this function:

real (kind=8) function diffusion_pol_peak_factor ( real (kind=8), dimension(2), intent(in) x )

Calculates the poloidal envelope of the anomalous transport By default, anomalous transport is a flux-function similar to 1D transport models. A ballooning structure can be added through the ballooning angle and the ballooning factor.

Parameters

[in] x Input (R,Z) coordinates, real(8)

Here is the call graph for this function:

Here is the caller graph for this function:

subroutine diffusion_solve	(	integer	nn,
		real (8), dimension(nn,diff_timestepper%blocksize)	XX_in,
		real(8)	dt
	)

Here is the call graph for this function:

Here is the caller graph for this function:

subroutine formrhsfunctionlocal	(	type(xgc_ts)	a_ts,
			time,
			ts_it,
			snes_it,
		real (kind=8), dimension(nn,a_ts%blocksize), intent(in)	XX_in,
		real (kind=8), dimension(nn), intent(in)	div_gamma_in,
		real (kind=8), dimension(nn,a_ts%blocksize), intent(out)	rhs_out,
		integer	nn
	)

Computations in XGC space for RHS evaluation This includes 4 nonlinear terms for each species, one in the momentum equation, and three in the temperature equation. The terms are: (1/n) grad(n).(D+eta).grad(u) = (1/n) (D+eta) (dn/dr)(du/dr) in the momentum equation, and (T/n) div(D.grad(n)) = (T/n) d(D dn/dr)/dr (1/3n) grad(n).(5D+2chi).grad(T) = (5D+2chi)/(3n) (dn/dr)(dT/dr) (2m/3) grad(u).eta.grad(u) = (2m eta)/3 (du/dr)^2 Since this involves only radial gradients, we can simply use the XGC matrix gridgradientx. We have to take care, though, that vertices with undefined grad(psi) do not contribute (since we defined the tensor diffusivity to be D_ij=D(psi) psi_hat psi_hat).

Parameters

[in,out]	ts	PETSc time stepping object, TS
[in]	time	Time stamp, PETScReal, PETScReal
[in]	ts_it	TS time step index, PETScInt
[in]	snes_it	SNES iteration index, PETScInt
[in]	XX_in	Input quantities [n,ui,Tipa,Tipe,{ue,Tepa,Tepe}], real(8)
[in]	div_gamma_in	div(D.grad(n)-n*v_pinch)
[out]	rhs_out	Nonlinear RHS terms [n,ui,Tipa,Tipe,{ue,Tepa,Tepe}], real(8)
[in]	nn	Number of mesh vertices, integer

Here is the call graph for this function:

Here is the caller graph for this function:

subroutine formrhsjacobian	(		ts,
			t_dummy,
			a_XX,
			J,
			Jpre,
		type(xgc_ts)	a_ts,
		intent(out)	ierr
	)

Update the RHS Jacobian In case the RHS Jacobian has any time dependent terms, this routine would compute the time dependent terms and put them into the final Jacobian for the present stage/step.

Parameters

[in]	ts	PETSc time stepping object, TS
[in]	t_dummy	Time stamp, PETScReal
[in]	a_XX	Current fields, Vec
[in,out]	J	Jacobian, Mat
[in,out]	Jpre	Preconditioned Jacobian, Mat
[in,out]	a_ts	XGC time stepping object, type(xgc_ts)
[out]	ierr	Error code, PETScErrorCode

Here is the call graph for this function:

Here is the caller graph for this function:

subroutine formrhsjacobianlocal	(	type(xgc_ts), intent(inout)	a_ts,
		intent(inout)	Jpre,
		real (kind=8), dimension(nn,a_ts%blocksize), intent(in)	XX_in,
		integer	nn,
		intent(inout)	ierr
	)

Helper routine in XGC space for setting up the non-linear terms of the RHS Jacobian. This routine is used to compute any time dependent terms on the XGC solver grid. The result of this calculation will be inserted in the final RHS Jacobian.

Parameters

[in,out]	a_ts	type(xgc_ts), XGC ts_object with grid information, etc.
[in,out]	Jpre	PETSc Mat, the RHS Jacobian matrix
[in]	n	real(8), perturbed electron density
[in]	ui	real(8), A_parallel
[in]	Ti	real(8), electrostatic potential
[in]	ue	real(8), del^2(A_parallel)
[in]	Te	real(8), del^2(A_parallel)
[in]	nn	integer, mesh size
[in,out]	ierr	PetscErrorCode

subroutine initialize_diffusion	(	integer, dimension(grid_global%nnode), intent(in)	bd,
		integer, intent(in)	is_update
	)

Here is the call graph for this function:

Here is the caller graph for this function:

subroutine rhsfunction	(		ts,
			time,
			a_XX,
			a_FF,
		type(xgc_ts)	a_ts,
		intent(out)	ierr
	)

Evaluates the RHS equation.

Parameters

[in,out]	ts	PETSc time stepping object, TS
[in]	time	Time stamp, PETScReal
[in]	a_XX	Current field data, Vec
[out]	a_FF	RHS result vecgtor, Vec
[in,out]	a_ts	XGC time stepping object, xgc_ts
[in,out]	ierr	PETScErrorCode

Here is the call graph for this function:

Here is the caller graph for this function:

subroutine ts_init	(	integer, dimension(grid_global%nnode), intent(in)	a_bc,
		type(xgc_ts)	a_ts,
		logical, intent(in)	is_update
	)

Initializes the PETSc time stepper for the 2D diffusion solver. This routine sets up a system of conserving Fick's law type equations on the 2D XGC solver mesh for: density, flow and parallel and perpendicular temperature, i.e., 3*n_species+1 equations. The linear terms of the form \(\nabla \cdot \boldsymbol{D}.\nabla X \) are discretized with linear finite elements. The nonlinear terms are discretized with finite difference. The diffusivity tensor is set up such that only trnasport perpendicular to flux-surfaces is computed by this model.

Parameters

[in]	a_bc	Boundary vertices for solver
[in,out]	a_ts	XGC time-stepper structure, type(xgc_ts)

Here is the call graph for this function:

Here is the caller graph for this function:

subroutine ts_solve	(	type(xgc_ts), intent(inout)	a_ts,
		real(kind=8), intent(in)	a_dt,
		real(kind=8), dimension(a_ts%nnode,blocksize), intent(inout)	XX_in,
		intent(in)	blocksize
	)

This routine performs the actual time integration of the 2D diffusion model.

Parameters

[in,out]	a_ts	XGC time-stepper structure, type(xgc_ts)
[in]	a_dt	Time step, real8
[in,out]	XX_in	Input moments (density, etc.), real8
[in]	blocksize	Number of equations, integer

Here is the call graph for this function:

Here is the caller graph for this function:

subroutine update_diffusion_eq_ftn	(	integer, intent(in)	n_species,
		integer, intent(in)	npsi_in,
		real (kind=8), dimension(npsi_in), intent(in)	psi_in,
		real (kind=8), dimension(npsi_in,n_species,4), intent(in)	diff_coeff_in
	)

Here is the call graph for this function:

Here is the caller graph for this function:

Functions/Subroutines

Function/Subroutine Documentation