"(D)irichlet (B)oundary (C)onditions" A module for evaluating Dirichlet boundary conditions for the Fourier decomposed Ampere and Poisson equations.
More...
|
| subroutine, public | dbc_weights (weights, R, Z, n, grid) |
| | Returns weights \( w_i(R,Z) \) for approximating the integral \( \Phi(R,Z)=\int_{\Omega'}\frac{R' f(R',Z')}{\sqrt{R'^2+R^2+(Z-Z')^2}}g(k,n)dR'dZ' \) as \( \Phi(R,Z)\approx\sum_{i=1}^{n_{\textrm{nodes}}} w_i f_i \). Here \( g(k,n)=\int_0^{2\pi}\frac{\cos(nx)}{\sqrt{1-k\cos(x)}}dx \) and \( k(R,Z,R',Z')=\frac{2RR'}{R^2+R'^2+(R-R')^2} \). The data \( f(R',Z') \) is assumed piecewise linear over the triangulation of the domain \( \Omega \) and Gauss quadrature is used for the \( dR'dZ' \) integral. More...
|
| |
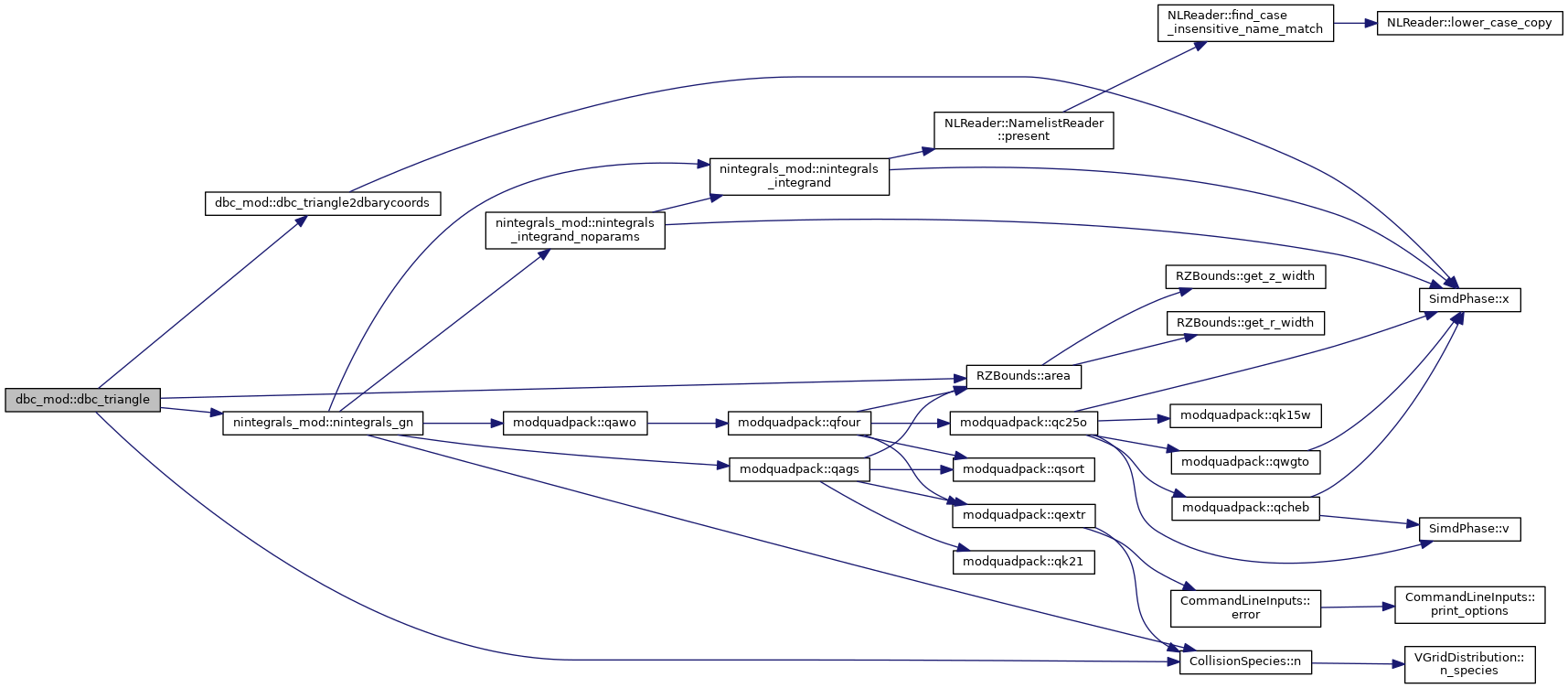
| real(kind=8) function, public | dbc_triangle (R, Z, RS, ZS, FS, n) |
| | Evaluates the integral \( Phi(R',Z')=\int_{\Delta}\frac{R' f(R',Z')}{\sqrt{R'^2+R^2+(Z-Z')^2}}g(k,n)dR'dZ' \) where \( g(k,n)=\int_0^{2\pi}\frac{\cos(nx)}{\sqrt{1-k\cos(x)}}dx \) and \( k(R,Z,R',Z')=\frac{2RR'}{R^2+R'^2+(R-R')^2} \) using linear interpolation for the data \( f(R',Z') \) over the triangle \( \Delta \) and Gauss quadrature for the \( dR'dZ' \) integral. More...
|
| |
|
| integer, parameter | ngauss =6 |
| | number of points for the Gauss-quadrature over a unit triangle More...
|
| |
| real(kind=8), parameter | pi = 4*atan(1.0D0) |
| | value for pi used inside the module. More...
|
| |
real(kind=8), dimension(6),
parameter | xi =(/ 0.816847572980459D0, 0.091576213509771D0, 0.091576213509771D0, 0.108103018168070D0, 0.445948490915965D0, 0.445948490915965D0 /) |
| | x coordinates for the Gauss-quadrature over a unit triangle More...
|
| |
real(kind=8), dimension(6),
parameter | yi =(/ 0.091576213509771D0, 0.816847572980459D0, 0.091576213509771D0, 0.445948490915965D0, 0.108103018168070D0, 0.445948490915965D0 /) |
| | y coordinates for the Gauss-quadrature over a unit triangle More...
|
| |
real(kind=8), dimension(6),
parameter | wi =(/ 0.109951743655322D0, 0.109951743655322D0, 0.109951743655322D0, 0.223381589678011D0, 0.223381589678011D0, 0.223381589678011D0 /) |
| | weight for the Gauss point in Gauss-quadrature over a unit triangle More...
|
| |
"(D)irichlet (B)oundary (C)onditions" A module for evaluating Dirichlet boundary conditions for the Fourier decomposed Ampere and Poisson equations.
- Author
- Eero Hirvijoki
| real(kind=8) function, public dbc_mod::dbc_triangle |
( |
real(kind=8), intent(in) |
R, |
|
|
real(kind=8), intent(in) |
Z, |
|
|
real(kind=8), dimension(3), intent(in) |
RS, |
|
|
real(kind=8), dimension(3), intent(in) |
ZS, |
|
|
real(kind=8), dimension(3), intent(in) |
FS, |
|
|
integer, intent(in) |
n |
|
) |
| |
Evaluates the integral \( Phi(R',Z')=\int_{\Delta}\frac{R' f(R',Z')}{\sqrt{R'^2+R^2+(Z-Z')^2}}g(k,n)dR'dZ' \) where \( g(k,n)=\int_0^{2\pi}\frac{\cos(nx)}{\sqrt{1-k\cos(x)}}dx \) and \( k(R,Z,R',Z')=\frac{2RR'}{R^2+R'^2+(R-R')^2} \) using linear interpolation for the data \( f(R',Z') \) over the triangle \( \Delta \) and Gauss quadrature for the \( dR'dZ' \) integral.
- Author
- Eero Hirvijoki
- Parameters
-
| [in] | R | cylindrical R for the position where to evaluate the integral |
| [in] | Z | cylindrical Z for the position where to evaluate the integral |
| [in] | RS | cylindrical R for the triangle vertices |
| [in] | ZS | cylindrical Z for the triangle vertices |
| [in] | FS | the function \( f(R,Z) \) values at the triangle vertices |
| [in] | n | the mode number for the toroidal angular integrals. |
- Todo:
- Right now I'm not aware of anything that should be improved.
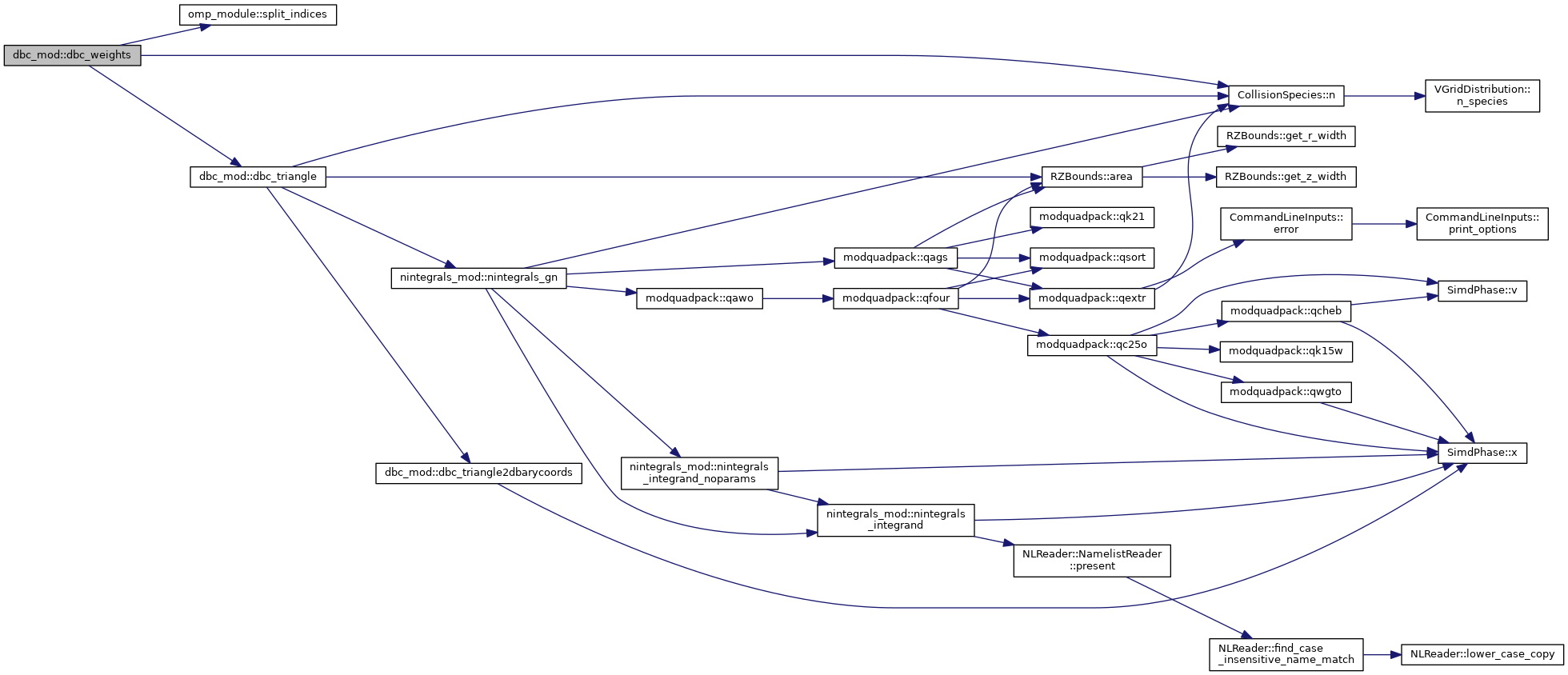
| real(kind=8) function, dimension(3) dbc_mod::dbc_triangle2dbarycoords |
( |
real(kind=8), dimension(3), intent(in) |
xs, |
|
|
real(kind=8), dimension(3), intent(in) |
ys, |
|
|
real(kind=8), intent(in) |
x, |
|
|
real(kind=8), intent(in) |
y |
|
) |
| |
|
private |
| subroutine, public dbc_mod::dbc_weights |
( |
real(kind=8), dimension(grid%nnode), intent(out) |
weights, |
|
|
real(kind=8), intent(in) |
R, |
|
|
real(kind=8), intent(in) |
Z, |
|
|
integer, intent(in) |
n, |
|
|
type(grid_type), intent(in) |
grid |
|
) |
| |
Returns weights \( w_i(R,Z) \) for approximating the integral \( \Phi(R,Z)=\int_{\Omega'}\frac{R' f(R',Z')}{\sqrt{R'^2+R^2+(Z-Z')^2}}g(k,n)dR'dZ' \) as \( \Phi(R,Z)\approx\sum_{i=1}^{n_{\textrm{nodes}}} w_i f_i \). Here \( g(k,n)=\int_0^{2\pi}\frac{\cos(nx)}{\sqrt{1-k\cos(x)}}dx \) and \( k(R,Z,R',Z')=\frac{2RR'}{R^2+R'^2+(R-R')^2} \). The data \( f(R',Z') \) is assumed piecewise linear over the triangulation of the domain \( \Omega \) and Gauss quadrature is used for the \( dR'dZ' \) integral.
- Author
- Eero Hirvijoki
- Parameters
-
| [out] | weights | the precomputed weights for evaluating the integral |
| [in] | R | cylindrical R of the position for which the weights are precomputed |
| [in] | Z | cylindrical Z of the position for which the weights are precomputed |
| [in] | n | the mode number for the angular integrals. |
| [in] | grid | the structure containing the mesh and connectivity |
- Todo:
- Right now I'm not aware of anything that should be improved.
| integer, parameter dbc_mod::ngauss =6 |
|
private |
number of points for the Gauss-quadrature over a unit triangle
| real(kind=8), parameter dbc_mod::pi = 4*atan(1.0D0) |
|
private |
value for pi used inside the module.
| real(kind=8), dimension(6), parameter dbc_mod::wi =(/ 0.109951743655322D0, 0.109951743655322D0, 0.109951743655322D0, 0.223381589678011D0, 0.223381589678011D0, 0.223381589678011D0 /) |
|
private |
weight for the Gauss point in Gauss-quadrature over a unit triangle
| real(kind=8), dimension(6), parameter dbc_mod::xi =(/ 0.816847572980459D0, 0.091576213509771D0, 0.091576213509771D0, 0.108103018168070D0, 0.445948490915965D0, 0.445948490915965D0 /) |
|
private |
x coordinates for the Gauss-quadrature over a unit triangle
| real(kind=8), dimension(6), parameter dbc_mod::yi =(/ 0.091576213509771D0, 0.816847572980459D0, 0.091576213509771D0, 0.445948490915965D0, 0.108103018168070D0, 0.445948490915965D0 /) |
|
private |
y coordinates for the Gauss-quadrature over a unit triangle
The documentation for this module was generated from the following file:
- /u/gitlab-xgc/builds/YGMz2TJ8/0/xgc/XGC-Devel/XGC_core/dbc.F90


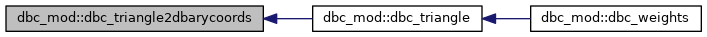
 1.8.5
1.8.5