#include <poly_basis.hpp>
Public Member Functions | |
| View< double ***, CLayout, Device > | compute_inner_product (const View< double ***, CLayout, Device > &dist_in) const |
| PolynomialBasisDistribution< Device > | get_coefficients (const View< double ***, CLayout, Device > &inner_prod_matrix) const |
| template<typename F > | |
| void | add_basis (int &basis_ind, F func) |
| template<typename... Fs> | |
| PolynomialBasis (const UniformRange &xrange_in, const UniformRange &yrange_in, Fs... funcs) | |
| PolynomialBasisDistribution< Device > | get_distribution (const View< double ***, CLayout, Device > &dist_in) const |
| template<typename F > | |
| View< double **, CLayout, Device > | get_moments (const int nnode, F lambda_func) const |
| View< double ***, CLayout, Device > | get_scaling (const PolynomialBasisDistribution< Device > &polynom, const View< double **, CLayout, Device > &g_mom) const |
Private Types | |
| using | exec_space = typename Device::execution_space |
Private Attributes | |
| int | n_poly |
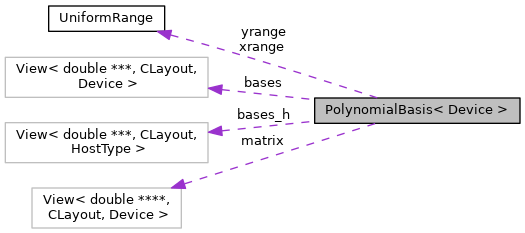
| UniformRange | xrange |
| UniformRange | yrange |
| View< double ***, CLayout, Device > | bases |
| View< double ***, CLayout, HostType > | bases_h |
| View< double ****, CLayout, Device > | matrix |
Member Typedef Documentation
◆ exec_space
|
private |
Constructor & Destructor Documentation
◆ PolynomialBasis()
|
inline |
Constructor for a polynomial basis with one polynomial per provided function, evaluated with the range and resolution specified by xrange_in and yrange_in. The resulting basis will be able to evaluate all given functions at any point within the specified ranges.
- Parameters
-
[in] xrange_in A uniform range object specifying the interval on which the polynomials should have support in the first dimension [in] yrange_in A uniform range object specifying the interval on which the polynomials should have support in the second dimension [in] funcs The desired basis functions on two dimensions

Member Function Documentation
◆ add_basis()
|
inline |
Adds a new basis for the polynomial representation
- Parameters
-
[in,out] basis_ind Offset index that is incremented so that the next basis is added to the next index in bases_h [in] func Function representating the new basis on two dimensions (x, y)


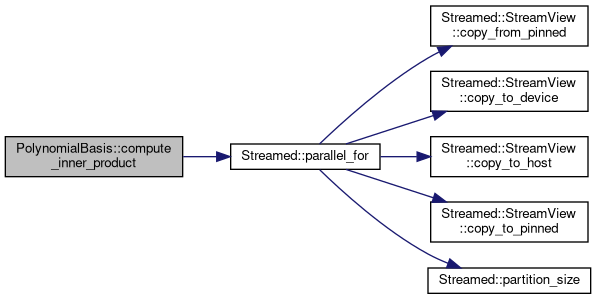
◆ compute_inner_product()
|
inline |
Sets up a moment matrix of the current plasma distribution function and computes orthonormal polynomial basis for scaling of the plasma distribution function Polynomials: lambda_i = sum_[j=1]^4 c_[i,j] gamma_j where gamma_1 = 1, gamma_2 = v_||, gamma_3 = v_pe, gamma_4 = v_||^2, gamma_5 = v_pe^2 Inner product <lambda_i,lambda_j> = int[lambda_i lambda_j f d^3 v] Moment matrix defined by inner products <gamma_i,gamma_j> Gamma = | <1,1> <1 ,v_||> <1 ,v_pe> <1 ,v_||^2> <1 ,v_pe^2> | | <v_||,v_||> <v_||,v_pe> <v_|| ,v_||^2> <v_|| ,v_pe^2> | | <v_pe,v_pe> <v_pe ,v_||^2> <v_pe ,v_pe^2> | | <v_||^2,v_||^2> <v_||^2,v_pe^2> | | <v_pe^2,v_pe^2> | or Gamma = | <1,1> <1 ,v_||> <1 ,v_||^2> <1 ,v_pe^2> | | <v_||,v_||> <v_|| ,v_||^2> <v_|| ,v_pe^2> | | <v_||^2,v_||^2> <v_||^2,v_pe^2> | | <v_pe^2,v_pe^2> |
===> <lambda_i,lambda_j> = sum_[k,l=1]^5 c_[i,k] Gamma_[k,l] c_[j,l] ==> lambda_i^T.A.lambda_k The coefficients c_[i,l] are calculated with Gram-Schmidt process lambda_i = gamma_i - sum_[j=1]^[i-1] <gamma_i,lambda_j>/<lambda_j,lambda_j> lambda_j
The coefficients of the basis polynomials are stored in a 4x4 matrix, The inner products in the matrix A are stored in a 10-element vector starting with the main diagonal, then going through the upper side diagonals.
The moments in the matrix Gamma are evaluated from the global variable storing the distribution function --> f0_f
The coefficients c_[i,j] of the basis polynomials are stored in a PolynomialBasisDistribution struct.
- Parameters
-
[in] dist_in The distribution function to be represented by polynomials return The inner product representation of dist_in

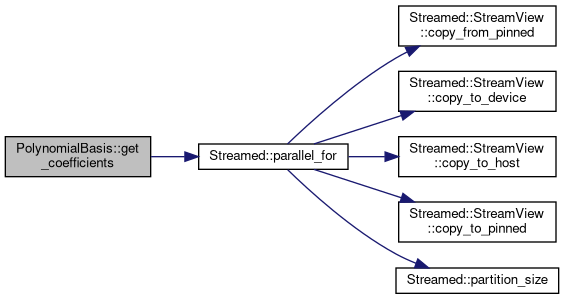
◆ get_coefficients()
|
inline |
Given the inner product matrix built from an input distribution, calculate and return the distribution with polynomial representation
- Parameters
-
[in] inner_prod_matrix The inner product matrix
- Returns
- The polynomial representation of the distribution used to calculate the inner product matrix

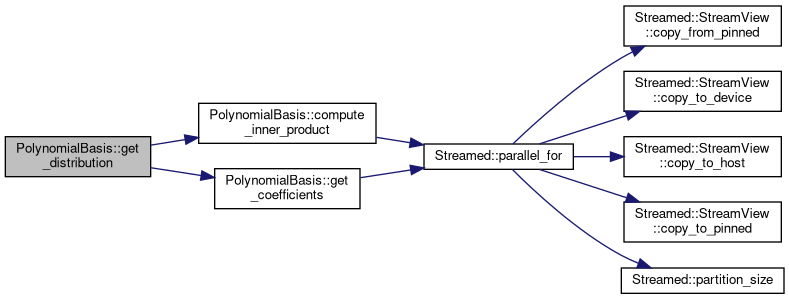
◆ get_distribution()
|
inline |
Constructs a polynomial representation of the input distribution
- Parameters
-
[in] dist_in The distribution function to be represented by polynomials return The polynomial representation of the distribution used to calculate the inner product matrix

◆ get_moments()
|
inline |
Computes moments of the distribution using a user-defined kernel function
- Parameters
-
[in] nnode Number of mesh nodes to loop over [in] lambda_func User defined kernel function for a single mesh node return The array of new moments

◆ get_scaling()
|
inline |

Member Data Documentation
◆ bases
|
private |
◆ bases_h
|
private |
◆ matrix
|
private |
◆ n_poly
|
private |
◆ xrange
|
private |
◆ yrange
|
private |
The documentation for this class was generated from the following file:
- /p/test_ssd/builds/t3_84szKM/0/xgc/XGC-Devel/XGC_core/cpp/poly_basis.hpp